Cho các hàm số phân thức hữu tỉ sau:
(3) ;
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Cho các hàm số phân thức hữu tỉ sau:
(3) ;
a) Tìm đạo hàm cấp một của các hàm số trên.
b) Tìm các đường tiệm cận của đồ thị các hàm số trên.
c) Vẽ đồ thị của các hàm số trên.
Quảng cáo
Trả lời:
(3)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
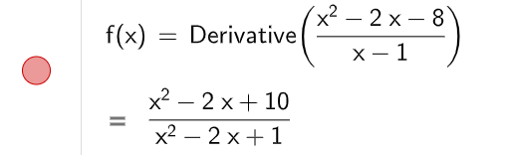
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
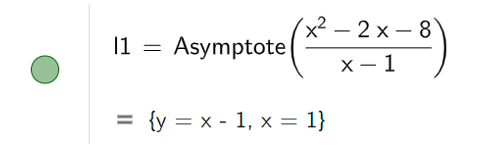
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
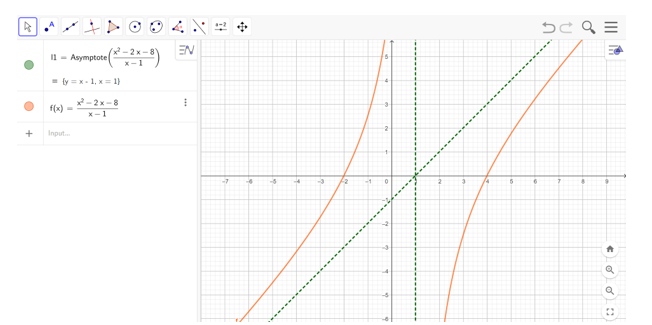
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
d) Để tìm giá trị lớn nhất của hàm số y = sin2x – x trên đoạn ta dùng lệnh Max(sin2x – x, ), kết quả thể hiện ở hình vẽ sau
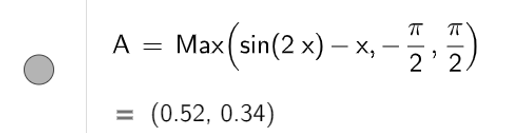
Vậy giá trị lớn nhất của hàm số là 0,34.
Để tìm giá trị nhỏ nhất của hàm số y = sin2x – x trên đoạn ta dùng lệnh Min( sin2x – x, ), kết quả thể hiện ở hình vẽ sau
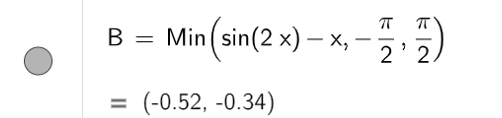
Vậy giá trị nhỏ nhất của hàm số là −0,34.
Lời giải
(3) y = x4 – 4x2 + 3
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative(x4 – 4x2 + 3), kết quả sẽ được hiển thị như hình bên dưới
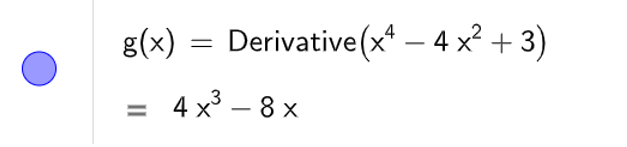
Để tính đạo hàm cấp hai ta dùng lệnh Derivative(x4 – 4x2 + 3, 2), kết quả sẽ được hiển thị như hình bên dưới
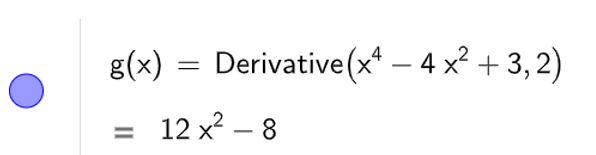
b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum(x4 – 4x2 + 3), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số y = x4 – 4x2 + 3 vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
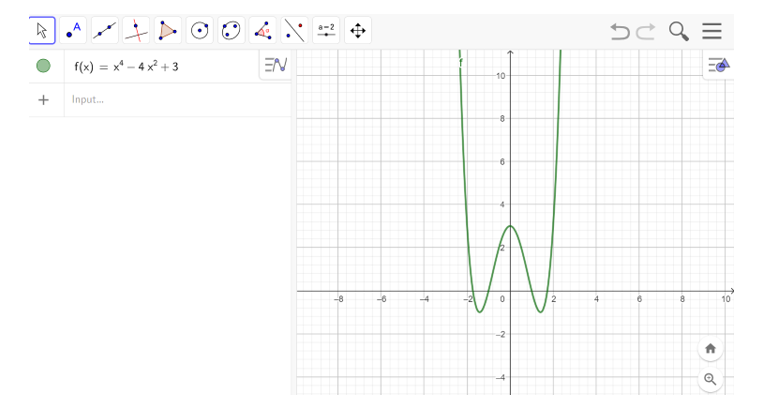
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.