Giải SGK Toán 12 KNTT Khảo sát và vẽ đồ thị hàm số với phần mềm Geogebra có đáp án
42 người thi tuần này 4.6 473 lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 3
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 2
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 1
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 3
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
(1) .
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới

Để tính đạo hàm cấp hai ta dùng lệnh Derivative( , 2), kết quả sẽ được hiển thị như hình bên dưới
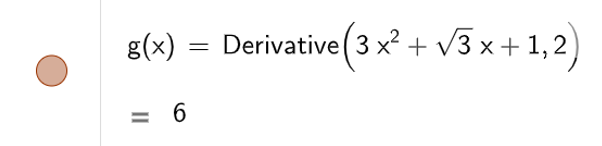
b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum( ), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số vào ô lệnh , màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
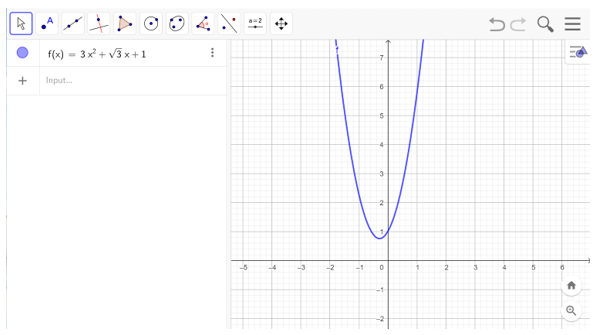
Lời giải
(2) y = x3 – 6x2 + 9
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative(x3 – 6x2 + 9), kết quả sẽ được hiển thị như hình bên dưới
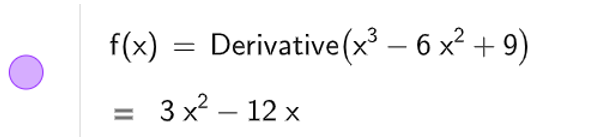
Để tính đạo hàm cấp hai ta dùng lệnh Derivative(x3 – 6x2 + 9, 2), kết quả sẽ được hiển thị như hình bên dưới

b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum(x3 – 6x2 + 9), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số y = x3 – 6x2 + 9 vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
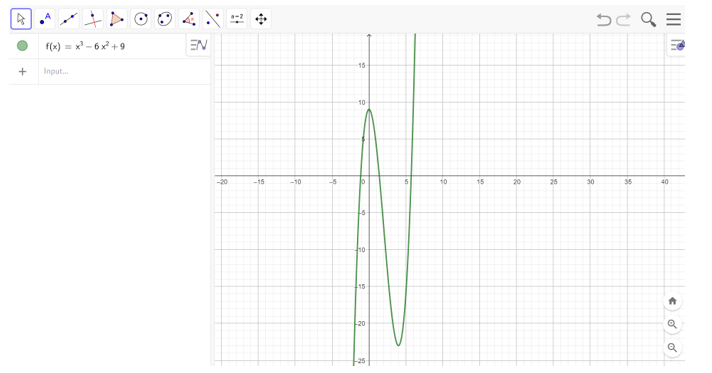
Lời giải
(3) y = x4 – 4x2 + 3
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative(x4 – 4x2 + 3), kết quả sẽ được hiển thị như hình bên dưới
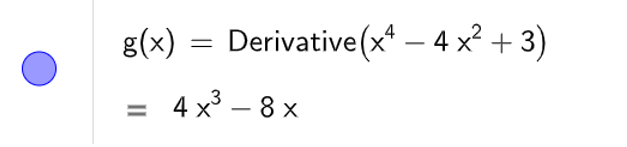
Để tính đạo hàm cấp hai ta dùng lệnh Derivative(x4 – 4x2 + 3, 2), kết quả sẽ được hiển thị như hình bên dưới
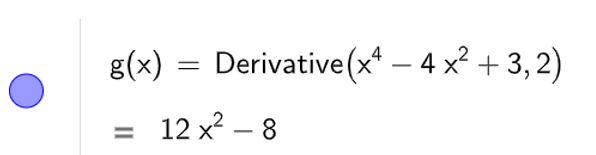
b) Để tìm cực trị của hàm số, ta dùng lệnh Extremum(x4 – 4x2 + 3), kết quả sẽ được hiển thị như hình sau

c) Nhập hàm số y = x4 – 4x2 + 3 vào ô lệnh, màn hình sẽ hiển thị đồ thị của hàm số cần vẽ như hình bên dưới
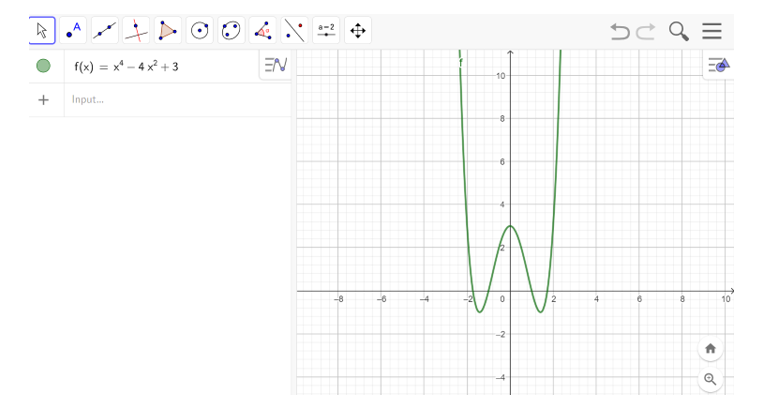
Lời giải
(1)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
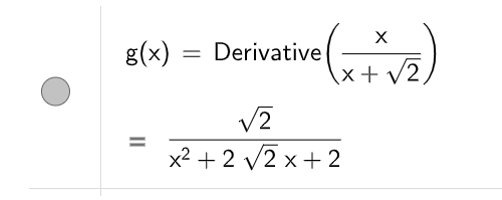
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
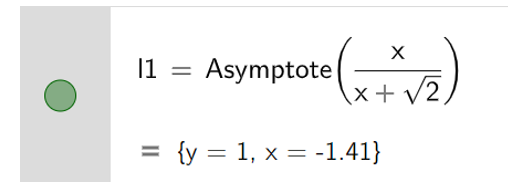
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
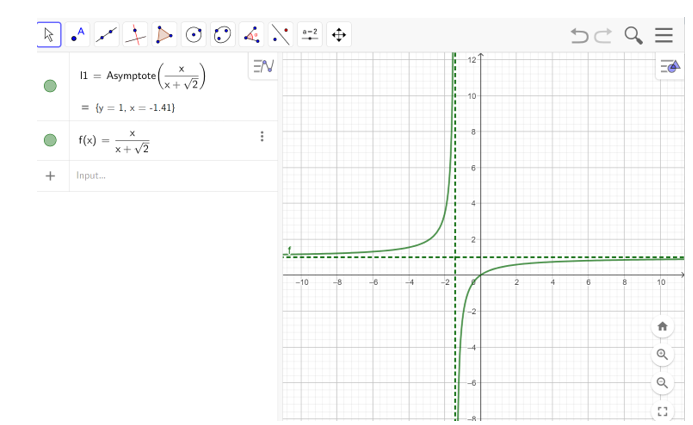
Lời giải
(2)
a) Để tính đạo hàm cấp một ta dùng lệnh Derivative( ), kết quả sẽ được hiển thị như hình bên dưới
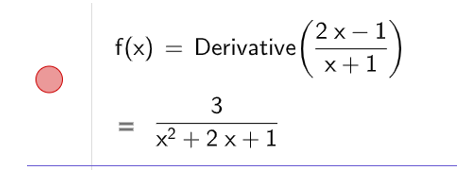
b) Để tìm đường tiệm cận của đồ thị hàm số, ta nhập lệnh Asymptote( ), kết quả được hiển thị như hình bên dưới
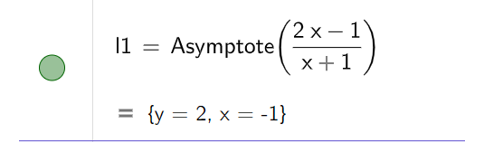
c) Bước 1: Vẽ tiệm cận của đồ thị hàm số bằng cách nhập câu lệnh Asymptote( ).
Bước 2: Vẽ đồ thị hàm số bằng cách nhập hàm số vào ô lệnh. Kết quả được hiển thị như hình bên dưới
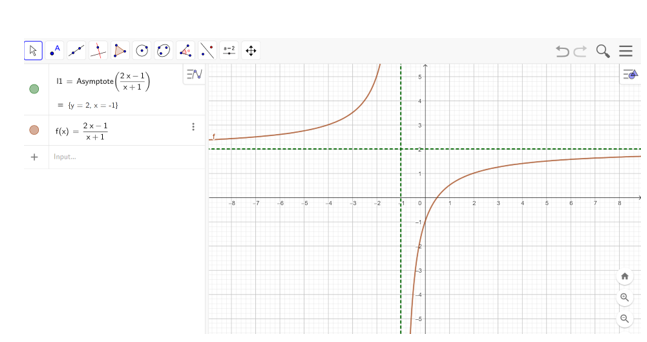
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.