Đề kiểm tra Ôn tập chương 4 (có lời giải) - Đề 2
4.6 0 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Tích phân (có lời giải) - Đề 3
39 lượt thi
22 câu hỏi
Đề kiểm tra Tích phân (có lời giải) - Đề 2
39 lượt thi
22 câu hỏi
Đề kiểm tra Tích phân (có lời giải) - Đề 1
46 lượt thi
22 câu hỏi
Đề kiểm tra Nguyên hàm (có lời giải) - Đề 3
125 lượt thi
22 câu hỏi
Đề kiểm tra Nguyên hàm (có lời giải) - Đề 2
126 lượt thi
22 câu hỏi
Đề kiểm tra Nguyên hàm (có lời giải) - Đề 1
189 lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 1
1.6 K lượt thi
22 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 12 Chân trời sáng tạo có đáp án - Đề 9
1.4 K lượt thi
22 câu hỏi
Danh sách câu hỏi:
Câu 1
A. \[F\left( x \right) = 2{x^3} + C\].
B. \[F\left( x \right) = \frac{2}{3}{x^3}\].
C. \[F\left( x \right) = \frac{{{x^3}}}{3} + C\].
D. \[F\left( x \right) = \frac{2}{3}{x^3} + C\].
Lời giải
Chọn D.
Ta có: \(\int {2{x^2}dx} = 2\int {{x^2}dx = 2.\frac{{{x^3}}}{3} + C = \frac{{2{x^3}}}{3} + C.} \)Câu 2
A. \[F\left( x \right) = 2\cos x\].
B. \[F\left( x \right) = - 2\cos x\].
C. \[F\left( x \right) = {\sin ^2}x + C\].
D. \[F\left( x \right) = {\cos ^2}x\].
Lời giải
Chọn B.
Ta có: \(\int {2\sin xdx = 2\int {\sin xdx} } = 2.\left( { - \cos x} \right) = - 2\cos x.\)Câu 3
A. \(y = \frac{1}{x}\).
B. \(y = \frac{1}{{x\ln 10}}\).
C. \(y = \frac{{\ln 10}}{x}\).
D. \(y = \frac{1}{{x\log 10}}\).
Lời giải
Chọn B.
Ta có: \[F'\left( x \right) = \left( {\log x} \right)' = \frac{1}{{x\ln 10}}\] nên \[F\left( x \right)\] là một nguyên hàm của hàm số \[y = \frac{1}{{x\ln 10}}\]Câu 4
A. \(F\left( x \right) = \frac{{{e^{2x}}}}{2} + C\).
B. \[F\left( x \right) = 2{e^{2x}} + C\].
C. \[F\left( x \right) = {e^{2x}} + C\].
D. \[F\left( x \right) = 2{e^{2x}} + C\].
Lời giải
Chọn A.
Ta có: \[\int {{e^{2x}}dx = \int {{{\left( {{e^2}} \right)}^x}dx = \frac{{{{\left( {{e^2}} \right)}^x}}}{{\ln {e^2}}} + C = \frac{{{e^{2x}}}}{2} + C} } \].Câu 5
A. \(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \).
B. \(\int\limits_a^b {kdx} = k(b - a),\forall k \in \mathbb{R}\).
C. \(\int\limits_a^b {f(x)dx} = \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} \) với \(c \in \left[ {a;b} \right]\).
D. \(\int\limits_a^b {f(x)dx} = \int\limits_b^a {f(x)dx} \).
Lời giải
Chọn D.
Theo tính chất tích phân A,B,C đúng
Đáp án D sai vì: \(\int\limits_a^b {f(x)dx} = - \int\limits_b^a {f(x)dx} \).Câu 6
A. \(I = 6\).
B. \(I = 5\).
C. \(I = 2\).
D. \(I = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 32.
B. - 40.
C. 36.
D. 40
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \(I = 168\).
B. \(I = - 17\).
C. \(I = 31\).
D. \(I = 17\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(f\left( x \right) = 6{x^2} - 2 + x\).
B. \(f\left( x \right) = \frac{1}{2}{x^4} - {x^2} + x\).
C. \(f\left( x \right) = \frac{1}{2}{x^4} - {x^2} + x + C\).
D. \(f\left( x \right) = 6{x^2} - 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(V = \pi \int\limits_0^2 {{e^{2x}}} \;{\rm{d}}x\).
B. \(V = \int\limits_0^2 {{e^x}} \;{\rm{d}}x\).
C. \(V = \pi \int\limits_0^2 {{e^x}} \;{\rm{d}}x\).
D. \(V = \int\limits_0^2 {{e^{2x}}} \;{\rm{d}}x\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(s\left( t \right) = \int\limits_0^{\frac{{3\pi }}{4}} {\left( {1 + \sin t} \right)} {\rm{d}}t\).
B. \[s\left( t \right) = \int\limits_0^{\frac{{3\pi }}{4}} {{{\left( {1 + \sin t} \right)}^2}} {\rm{d}}t\].
C. \(s(t) = \left| {\int_0^{\frac{{3\pi }}{4}} {(1 - \cos t)} {\rm{d}}t} \right|\).
D. \(s(t) = v\left( {\frac{{3\pi }}{4}} \right) - v(0)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Có \(\int {\left( {f\left( x \right) - g\left( x \right)} \right)} {\rm{d}}x = F\left( x \right) - G\left( x \right) + C\).
Đúng
Sai
b) \(\int {g\left( x \right){\rm{d}}x} = {5^x}\ln 5 - {e^x} + {C_2}\).
Đúng
Sai
Đúng
Sai
d) Biết \(F\left( 0 \right) = 5;G\left( 0 \right) = \frac{1}{{\ln 5}} - 1\). Ta có \(F\left( 1 \right) - G\left( 1 \right) = \frac{{67}}{5} - \frac{5}{{\ln 5}} + e\).
Đúng
Sai
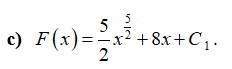
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
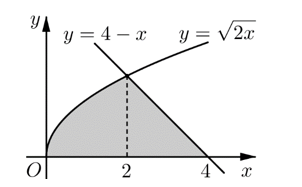
a. Hoành độ giao điểm của đồ thị hàm số \[y = \sqrt {2x} \] và \[y = 4 - x\] là \[x = 2\].
Đúng
Sai
b. Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = \sqrt {2x} \], trục hoành và hai đường thẳng \[x = 0,{\rm{ }}x = 2\] là \[{S_1} = \int\limits_0^2 {2xdx} \].
Đúng
Sai
c. Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = 4 - x\], trục hoành và hai đường thẳng \[x = 2,{\rm{ }}x = 4\] là \[{S_2} = \int\limits_0^2 {(x - 4)dx} \].
Đúng
Sai
d. Diện tích hình phẳng \[S\] giới hạn bởi các đồ thị hàm số \[y = \sqrt {2x} ,\] \[y = 4 - x\] và trục hoành \[Ox\] (như hình vẽ) được tính bởi công thức \[S = \int\limits_0^2 {\sqrt {2x} {\rm{d}}x} + \int\limits_2^4 {\left( {4 - x} \right){\rm{d}}x} .\]
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) \(\int\limits_0^2 {\left( {3{x^2} - 2{{\rm{e}}^x}} \right){\rm{d}}x} = 6 - 2{{\rm{e}}^2}\).
Đúng
Sai
b) Nước chảy từ đáy của một bồn chứa với tốc độ \(k\left( t \right) = 250 - 6t\) (lít/phút), trong đó \(0 \le t \le 45\). Lượng nước chảy ra khỏi bồn chứa trong \(10\) phút đầu tiên bằng \(2200\) (lít).
Đúng
Sai
c) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\left( {{{\tan }^2}x - {{\cot }^2}x} \right){\rm{d}}x} = a - \frac{b}{c}\sqrt 3 \) với \(a,\;b,\;c \in \mathbb{N},\;c \ne 0\) và \(\frac{b}{c}\) tối giản thì \(a + b + c = 9\).
Đúng
Sai
d) \(\int\limits_0^{\frac{\pi }{3}} {\left| {{{\cos }^2}x - \sin x\cos x} \right|{\rm{d}}x} = a + b\pi - c\sqrt 3 \) với \(a,\;b,\;c \in \mathbb{Q}\) thì \(a - c + b = \frac{5}{6}\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
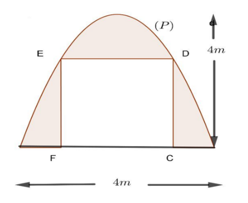
a) Chọn hệ trục tọa độ\[Oxy\], như hình vẽ thì phương trình của đường cong \[\left( P \right)\] cánh cổng là \[y = f\left( x \right) = - {x^2} + 4\].
Đúng
Sai
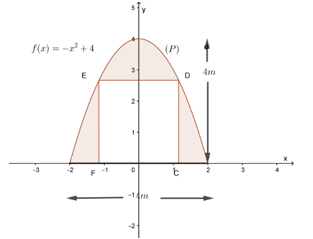
b) Nếu chiều cao cửa đi là \(CD = 2m\) thì chiều rộng của cửa là \(CF = 2\sqrt 2 m\).
Đúng
Sai
c) Nếu chiều cao cửa đi là \(CD = 2m\) thì chi phí để trang trí phần tô đậm là \[\left( {\frac{{32 - 6\sqrt 2 }}{3}} \right)\] triệu đồng.
Đúng
Sai
d) Số tiền ít nhất dùng để trang trí phần tô đậm ( làm tròn đến hàng nghìn đồng) là \[4.508.000\] đồng.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập