Một vật chuyển động với vận tốc \(v(t) = 1 + \sin t\,\,(\;{\rm{m/s}})\). Quãng đường vật di chuyển trong khoảng thời gian từ \(t = 0\) (giây) đến thời điểm \(t = \frac{{3\pi }}{4}\) (giây) được tính theo công thức
Một vật chuyển động với vận tốc \(v(t) = 1 + \sin t\,\,(\;{\rm{m/s}})\). Quãng đường vật di chuyển trong khoảng thời gian từ \(t = 0\) (giây) đến thời điểm \(t = \frac{{3\pi }}{4}\) (giây) được tính theo công thức
A. \(s\left( t \right) = \int\limits_0^{\frac{{3\pi }}{4}} {\left( {1 + \sin t} \right)} {\rm{d}}t\).
B. \[s\left( t \right) = \int\limits_0^{\frac{{3\pi }}{4}} {{{\left( {1 + \sin t} \right)}^2}} {\rm{d}}t\].
Câu hỏi trong đề: Đề kiểm tra Ôn tập chương 4 (có lời giải) !!
Quảng cáo
Trả lời:
Chọn A
Gọi \(s(t)\)là quãng đường mà vật di chuyển trong khoảng thời gian từ \(t = 0\) (giây) đến \(t = \frac{{3\pi }}{4}\) (giây). Mà \(s'(t) = v(t)\) nên ta có \(s(t) = \int_0^{\frac{{3\pi }}{4}} {(1 + \sin t)} {\rm{d}}t\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phần giải chi tiết
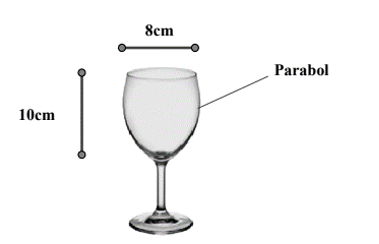
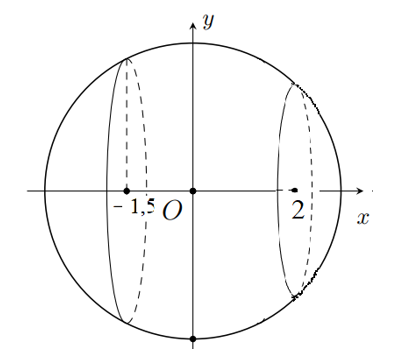
Trên hệ trục \[Oxy\] xét đường tròn \[(C)\]có phương trình \[{x^2} + {y^2} = 2,{5^2}\]. Khi đó nửa phần trên trục hoành của \[(C)\] có phương trình \[y = \sqrt {2,{5^2} - {x^2}} \]. Xét hình phẳng \[(H)\]giới hạn bởi nửa phần trên trục hoành của \[(C)\], trục \[Ox\] và các đường thẳng \[x = - 1,5,\,x = 2\]. Quay hình phẳng \[(H)\] quanh trục hoành ta được khối tròn xoay có thể tích bằng thể tích phần không gian phía trong của hầm biogas.
Thể tích phần không gian bên trong hầm biogas được tính bởi công thức \[V = \pi \int\limits_{ - 1,5}^2 {2,{5^2} - {x^2}} dx = \frac{{217}}{{12}}\pi \approx 56,8\]Lời giải
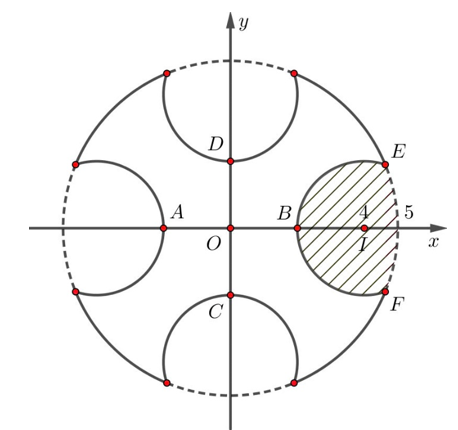
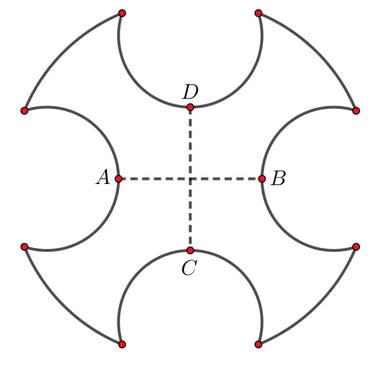
Chọn hệ toạ độ \[Oxy\] sao cho \[O\] trùng với giao điểm của \(AB\) và \(CD\); các tia lần lượt trùng với các tia \(OB\),\(OD\). Ta có:
Phương trình đường tròn lớn tâm \[O\] là: \({x^2} + {y^2} = 25 \Leftrightarrow y = \pm \sqrt {25 - {x^2}} \).
Phương trình đường tròn nhỏ tâm \[I\] là: \({\left( {x - 4} \right)^2} + {y^2} = 4 \Leftrightarrow y = \pm \sqrt {4 - {{\left( {x - 4} \right)}^2}} \).
Phương trình hoành độ giao điểm của 2 đường tròn là: \(4 - {\left( {x - 4} \right)^2} = 25 - {x^2} \Leftrightarrow x = \frac{{37}}{8}\).
Gọi \(S,{S_t},S'\) lần lượt là diện tích một mặt của chi tiết, diện tích đường tròn tâm \[O\] và diện tích phần gạch sọc.
Ta có: \(S = {S_t} - 4S' = 25\pi - 4.\left( {2\int\limits_2^{\frac{{37}}{8}} {\sqrt {4 - {{\left( {x - 4} \right)}^2}} dx + 2\int\limits_{\frac{{37}}{8}}^5 {\sqrt {25 - {x^2}} dx} } } \right)\)
Vậy chi phí để sơn hoàn thiện chi tiết máy là: \(x = S.2.1000 \approx 79,5\)( nghìn đồng).Câu 3
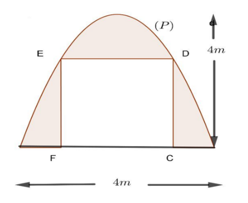
a) Chọn hệ trục tọa độ\[Oxy\], như hình vẽ thì phương trình của đường cong \[\left( P \right)\] cánh cổng là \[y = f\left( x \right) = - {x^2} + 4\].
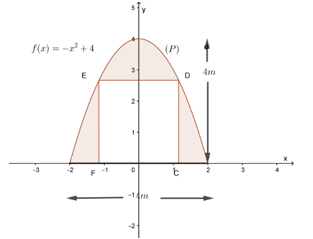
b) Nếu chiều cao cửa đi là \(CD = 2m\) thì chiều rộng của cửa là \(CF = 2\sqrt 2 m\).
c) Nếu chiều cao cửa đi là \(CD = 2m\) thì chi phí để trang trí phần tô đậm là \[\left( {\frac{{32 - 6\sqrt 2 }}{3}} \right)\] triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Có \(\int {\left( {f\left( x \right) - g\left( x \right)} \right)} {\rm{d}}x = F\left( x \right) - G\left( x \right) + C\).
b) \(\int {g\left( x \right){\rm{d}}x} = {5^x}\ln 5 - {e^x} + {C_2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
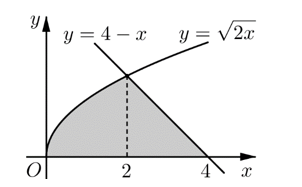
a. Hoành độ giao điểm của đồ thị hàm số \[y = \sqrt {2x} \] và \[y = 4 - x\] là \[x = 2\].
b. Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = \sqrt {2x} \], trục hoành và hai đường thẳng \[x = 0,{\rm{ }}x = 2\] là \[{S_1} = \int\limits_0^2 {2xdx} \].
c. Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = 4 - x\], trục hoành và hai đường thẳng \[x = 2,{\rm{ }}x = 4\] là \[{S_2} = \int\limits_0^2 {(x - 4)dx} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.