PHẦN 1: TƯ DUY ĐỊNH LƯỢNG

Lĩnh vực: Toán học (50 câu – 75 phút)

Câu 1. Theo thống kê về độ tuổi trung bình của một số đội tại giải U23 Châu Á năm 2018 và 2020, với trục tung là độ tuổi của các cầu thủ, trục hoành là thông tin thống kê từng năm, ta có biểu đồ như hình vē sau:

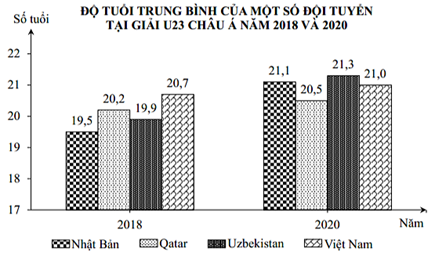
Trong năm 2018, đội tuyển nào dưới đây có trung bình cộng số tuổi cao nhất?

Hàm số \(f\left( x \right)\) có đúng một điểm cực trị khi và chỉ khi tam thức \(g\left( x \right) = {x^2} + 2mx + 5\) vô nghiệm hoặc có hai nghiệm phân biệt trong đó một nghiệm là \(x =  - 1\), hoặc \(g\left( x \right)\) có nghiệm kép.

Tức là \(\left[ {\begin{array}{*{20}{l}}{{{\Delta '}_g} < 0}\\{\left\{ {\begin{array}{*{20}{l}}{g( - 1) = 0}\\{\Delta ' > 0}\end{array}} \right.}\\{{{\Delta '}_g} = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 5 < 0}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2m + 6 = 0}\\{{m^2} - 5 > 0}\end{array}} \right.}\\{{m^2} - 5 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - \sqrt 5  \le m \le \sqrt 5 }\\{m = 3}\end{array}} \right.} \right.} \right..\)

Do đó tập các giá trị nguyên thỏa mãn yêu cầu bài toán là \(S = \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3} \right\}.\)

Đáp án: 6.

Năm 2021 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot \left( {1 - 0,02} \right) = 850 \cdot 0,98\) (triệu đồng).

Năm 2022 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^2}\) (triệu đồng).

Năm 2023 hãng xe ô tô niêm yết giá bán xe X là: \[850 \cdot 0,{98^3}\] (triệu đồng).

Năm 2024 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^4}\) (triệu đồng).

Năm 2025 hãng xe ô tô niêm yết giá bán xe X là:

\(850 \cdot 0,{98^5} = 768,3326 \approx 768,333\) (triệu đồng).

Vậy 2025 hãng xe ô tô niêm yết giá bán xe X là \[768\,\,333\,\,000\] đồng. Chọn A.