Câu hỏi:
20/06/2024 200
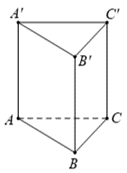
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \[ABC\] là tam giác vuông tại \(B\) với \(AB = 6\,,\,\,BC = 3\) và \(AA' = 12.\) Gọi \(M\) là trung điểm của cạnh \[AB.\] Khoảng cách giữa hai đường thẳng \(AB'\) và \[CM\] là
Quảng cáo
Trả lời:
Giải bởi Vietjack
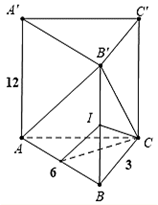
Gọi \(I\) là trung điểm \(BB'\), suy ra \(AB'\,{\rm{//}}\,MI\).
Xét mặt phẳng \((MIC)\) có \[MI\,{\rm{//}}\,AB' \Rightarrow AB'\,{\rm{//}}\,\left( {MIC} \right)\]
Mà \(CM \in (MIC)\) nên
\(d\left( {AB'\,;\,\,CM} \right) = d\left( {AB'\,;\,\,\left( {MIC} \right)} \right) = d\left( {A\,,\,\,\left( {MIC} \right)} \right)\)
Lại xét đoạn thẳng \(AB\) cắt \[\left( {MIC} \right)\] tại \(M\) với \(MA = MB\)
\( \Rightarrow d\left( {A\,,\,\,\left( {MIC} \right)} \right) = d\left( {B\,,\,\,\left( {MIC} \right)} \right)\)\[ \Rightarrow d\left( {AB'\,,\,\,CM} \right) = d\left( {B\,,\,\,\left( {MIC} \right)} \right).\]Mặt khác ta có tứ diện \(B.AB'C\) có \(BA\,,\,\,BB'\,,\,\,BC\) đôi một vuông góc nhau nên
\(\frac{1}{{d{{\left( {B\,,\,\,\left( {MIC} \right)} \right)}^2}}} = \frac{1}{{B{I^2}}} + \frac{1}{{B{M^2}}} + \frac{1}{{B{C^2}}} = \frac{1}{{{6^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{3^2}}} = \frac{1}{{{2^2}}}\)
\( \Rightarrow d\left( {B\,,\,\,\left( {MIC} \right)} \right) = 2 \Rightarrow d\left( {AB'\,,\,\,CM} \right) = d\left( {B\,,\,\,\left( {MIC} \right)} \right) = 2\).
Đáp án: 2.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm số \(f\left( x \right)\) có đúng một điểm cực trị khi và chỉ khi tam thức \(g\left( x \right) = {x^2} + 2mx + 5\) vô nghiệm hoặc có hai nghiệm phân biệt trong đó một nghiệm là \(x = - 1\), hoặc \(g\left( x \right)\) có nghiệm kép.
Tức là \(\left[ {\begin{array}{*{20}{l}}{{{\Delta '}_g} < 0}\\{\left\{ {\begin{array}{*{20}{l}}{g( - 1) = 0}\\{\Delta ' > 0}\end{array}} \right.}\\{{{\Delta '}_g} = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 5 < 0}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2m + 6 = 0}\\{{m^2} - 5 > 0}\end{array}} \right.}\\{{m^2} - 5 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - \sqrt 5 \le m \le \sqrt 5 }\\{m = 3}\end{array}} \right.} \right.} \right..\)
Do đó tập các giá trị nguyên thỏa mãn yêu cầu bài toán là \(S = \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3} \right\}.\)
Đáp án: 6.
Lời giải
Năm 2021 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot \left( {1 - 0,02} \right) = 850 \cdot 0,98\) (triệu đồng).
Năm 2022 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^2}\) (triệu đồng).
Năm 2023 hãng xe ô tô niêm yết giá bán xe X là: \[850 \cdot 0,{98^3}\] (triệu đồng).
Năm 2024 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^4}\) (triệu đồng).
Năm 2025 hãng xe ô tô niêm yết giá bán xe X là:
\(850 \cdot 0,{98^5} = 768,3326 \approx 768,333\) (triệu đồng).
Vậy 2025 hãng xe ô tô niêm yết giá bán xe X là \[768\,\,333\,\,000\] đồng. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận