Câu hỏi:
25/06/2024 119Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông tại \[A.\] Hình chiếu của \[S\] lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC,\,\,AB = a,\,\,AC = a\sqrt 3 ,\,\,SB = a\sqrt 2 .\) Thể tích của khối chóp \[S.ABC\]bằng
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
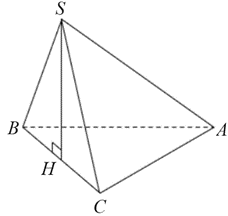
Xét tam giác \[ABC\] vuông tại \(A\) có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a.\)
Vì \(H\) là trung điểm của \[BC\] nên \(BH = a.\)
Xét tam giác \[SBH\] vuông tại \(H\) có:
\(SH = \sqrt {S{B^2} - H{B^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} - {a^2}} = a.\)Diện tích đáy \[ABC\] là: \({S_{ABC}} = \frac{1}{2}AB \cdot AC = \frac{1}{2}{a^2} \cdot \sqrt 3 .\)
Thể tích của khối chóp \[S.ABC\] là: \(V = \frac{1}{3}SH \cdot {S_{ABC}} = \frac{1}{3} \cdot a \cdot \frac{1}{2}{a^2}\sqrt 3 = \frac{{{a^3}\sqrt 3 }}{6}.\) Chọn C.
Nhà sách vietjack
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian \[Oxyz,\] cho mặt phẳng \((\alpha ):ax - y + 2z + b = 0\) đi qua giao tuyến của hai mặt phẳng \((P):x - y - z + 1 = 0\) và \((Q):x + 2y + z - 1 = 0.\) Giá trị của \(a + 4b\) bằng
Xem đáp án »
25/06/2024
13,076
Câu 2:
Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + \left( {5 - m} \right)x\) đồng biến trên khoảng \(\left( {2\,;\,\, + \infty } \right)\) là
Xem đáp án »
25/06/2024
9,837
Câu 3:
Biết \(M\left( {1\,;\,\, - 5} \right)\) là một điểm cực trị của hàm số \(y = f\left( x \right) = a{x^3} + 4{x^2} + bx + 1.\) Giá trị \(f\left( 2 \right)\) bằng
Xem đáp án »
25/06/2024
8,206
Câu 4:
Gọi \(g\left( x \right)\) là một nguyên hàm của hàm số \[f\left( x \right) = \ln \left( {x - 1} \right).\] Cho biết \(g\left( 2 \right) = 1\) và \(g\left( 3 \right) = a\ln b\) trong đó \[a,\,\,b\] là các số nguyên dương phân biệt. Giá trị của \(T = 3{a^2} - {b^2}\) là
Xem đáp án »
25/06/2024
7,434
Câu 5:
Cho các số thực dương \(x \ne 1\,,\,\,y \ne 1\) thỏa mãn \({\log _2}x = {\log _y}16\) và tích \(xy = 64.\) Giá trị của biểu thức \({\left( {{{\log }_2}\frac{x}{y}} \right)^2}\) là
Xem đáp án »
25/06/2024
6,573
Câu 6:
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Xem đáp án »
11/07/2024
5,327
Câu 7:
Trên mặt phẳng tọa độ \[Oxy,\] cho điểm \(P\left( { - 3\,;\,\, - 2} \right)\) và đường tròn \(\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 36.\) Từ điểm \(P\) kẻ các tiếp tuyến \[PM\] và \[PN\] tới đường tròn \(\left( C \right),\) với \[M,\,\,N\] là các tiếp điểm. Phương trình đường thẳng \[MN\] là
Xem đáp án »
25/06/2024
3,949
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 8)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận