Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 14)
70 người thi tuần này 4.6 2.8 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 31)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Danh sách câu hỏi:
Câu 1
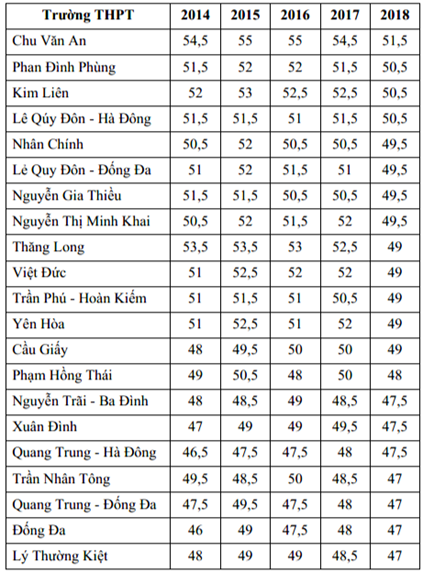
A. Lê Quý Đôn - Hà Đông.
B. Phan Đình Phùng.
Lời giải
Năm 2018 điểm đầu vào của trường THPT Lê Quý Đôn – Hà Đông là \[50,5.\]
Năm 2018 điểm đầu vào của trường THPT Phan Đình Phùng là \[50,5.\]
Năm 2018 điểm đầu vào của trường THPT Chu Văn An là \[51,5.\]
Năm 2018 điểm đầu vào của trường THPT Phạm Hồng Thái là 48.
Vậy năm 2018 điểm đầu vào của trường THPT Chu Văn An cao nhất.
Chọn C.
Lời giải
Ta có \(AB = \sqrt {26} \,,\,\,BC = \sqrt {104} = 2\sqrt {26} .\)
Gọi \[D\left( {x\,;\,\,y\,;\,\,z} \right)\], theo tính chất phân giác ta có \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{1}{2}.\)
Suy ra \(\overrightarrow {DA} = - \frac{1}{2}\overrightarrow {DC} & (*).\)
Ta có \(\overrightarrow {DA} = \left( {1 - x\,;\,\,2 - y\,;\,\, - 1 - z} \right)\) và \(\overrightarrow {DC} = \left( { - 4 - x\,;\,\,7 - y\,;\,\,5 - z} \right).\)
Do đó \((*) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{1 - x = - \frac{1}{2}\left( { - 4 - x} \right)}\\{2 - y = - \frac{1}{2}\left( {7 - y} \right)}\\{ - 1 - z = - \frac{1}{2}\left( {5 - z} \right)}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - \frac{2}{3}}\\{y = \frac{{11}}{3}}\\{z = 1}\end{array} \Rightarrow D\left( { - \frac{2}{3}\,;\,\,\frac{{11}}{3}\,;\,\,1} \right) \Rightarrow a + b + 2c = 5} \right.} \right..\)
Chọn A.
Câu 3
Lời giải
Vận tốc ô tô tại thời điểm bắt đầu phanh là \({v_1}\left( 5 \right) = 35\,\,(\;{\rm{m}}/{\rm{s}}).\)
Vận tốc của chuyển động khi phanh là \({v_2}(t) = - 70t + c.\)
Do \({v_2}\left( 0 \right) = 35\,\,(\;{\rm{m}}/{\rm{s}}) \Rightarrow c = 35 \Rightarrow {v_2}\left( t \right) = - 70t + 35.\)
Khi xe dừng hẳn tức là: \({v_2}\left( t \right) = 0 \Rightarrow - 70t + 35 = 0 \Leftrightarrow t = \frac{1}{2}{\rm{. }}\)
Quãng đường \(S\,\,\left( m \right)\) đi được ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là
\[S\,\,\left( m \right) = \int\limits_0^5 {7t} \,dt + \int\limits_0^{\frac{1}{2}} {\left( { - 70t + 35} \right)} \,dt = 96,25\,\,(\;{\rm{m}})\]. Chọn A.
Câu 4
Lời giải
Giả sử \(M\left( {a\,;\,\,b} \right)\), ta có:
\[\overrightarrow {AM} = \left( {a - 2\,;\,\,b - 1} \right) \Rightarrow 3\overrightarrow {AM} = \left( {3a - 6\,;\,\,3b - 3} \right)\]; \[\overrightarrow {AB} = \left( { - 3\,;\,\,6} \right)\]
\( \Rightarrow 3\overrightarrow {AM} + \overrightarrow {AB} = \left( {3a - 9\,;\,\,3b + 3} \right).\)
\(3\overrightarrow {AM} + \overrightarrow {AB} = \vec 0 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{3a - 9 = 0}\\{3b + 3 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 3}\\{b = - 1}\end{array} \Rightarrow M\left( {3\,;\,\, - 1} \right).} \right.} \right.\) Chọn D.
Câu 5
Lời giải
Ta có \(\left( {1 + i} \right)z + 2\bar z = 3 + 2i \Leftrightarrow \left( {1 + i} \right)\left( {a + bi} \right) + 2\left( {a - bi} \right) = 3 + 2i\)
\[ \Leftrightarrow \left( {3a - b} \right) + \left( {a - b} \right)i = 3 + 2i\]\( \Leftrightarrow \left\{ \begin{array}{l}3a - b = 3\\a - b = 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}3a - b = 3\\a - b = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3a - b = 3\\a - b = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = - \frac{3}{2}\end{array} \right.\).
Suy ra \(P = a + b = - 1\). Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \(\frac{1}{{32}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. \[11\,\,445\,\,000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. \(1\,\,360,3\,\;{\rm{c}}{{\rm{m}}^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
A. đề nghị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. từ ghép.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. mạnh dạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. cách mạng hóa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. chiến sĩ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. Cây thông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. tư duy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
A. văn học dân gian.
B. văn học viết.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trong từng vó ngựa tuần tra
Nòng súng chán làm sắt thép
Muốn thành cây để trổ hoa
Con suối riu riu trầm mặc
Đá hóa chàng trai mộng mơ
Cỏ cây rực màu thiếu nữ
Rừng buông sương tím ỡm ờ...
(Trần Đăng Khoa, Tây Bắc, https://ct.qdnd.vn)
Biện pháp tu từ nào được sử dụng trong câu thơ in đậm?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trong từng vó ngựa tuần tra
Nòng súng chán làm sắt thép
Muốn thành cây để trổ hoa
Con suối riu riu trầm mặc
Đá hóa chàng trai mộng mơ
Cỏ cây rực màu thiếu nữ
Rừng buông sương tím ỡm ờ...
(Trần Đăng Khoa, Tây Bắc, https://ct.qdnd.vn)
Biện pháp tu từ nào được sử dụng trong câu thơ in đậm?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
A. ngoại giao.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Nội dung nào sau đây không phải là xu thế phát triển của thế giới sau khi Chiến tranh lạnh chấm dứt?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
A. Kết hợp.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
A. \({6.10^5}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
A. \(0,60\mu {\rm{m}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
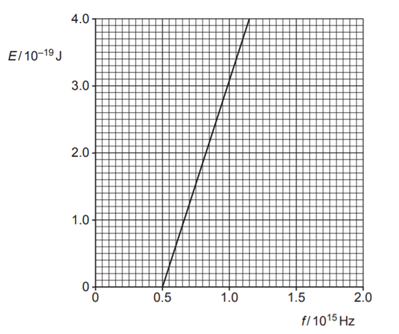
A. 6,2.10-34 J.s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
A. \(u = 120\cos \left( {100\pi t + \frac{\pi }{4}} \right)V.\)
B. \(u = 60\cos \left( {120\pi t + \frac{\pi }{4}} \right)V.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 113
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 115
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
A. (1) ADN mạch kép; (2) ARN mạch kép; (3) ADN mạch đơn; (4) ADN mạch đơn.
B. (1) ADN mạch kép; (2) ARN mạch đơn; (3) ADN mạch kép; (4) ARN mạch đơn.
C. (1) ADN mạch đơn; (2) ADN mạch kép; (3) ARN mạch đơn; (4) ARN mạch kép.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Một loạt đạn súng lớn văng vẳng dội đến ầm ĩ trên ngọn cây. Rồi loạt thứ hai...Việt ngóc dậy. Rõ ràng không phải tiếng pháo lễnh lãng của giặc. Đó là những tiếng nổ quen thuộc, gom vào một chỗ, lớn nhỏ không đều, chen vào đó là những dây súng nổ vô hồi vô tận. Súng lớn và súng nhỏ quyện vào nhau như tiếng mõ và tiếng trống đình đánh dậy trời đất hồi Đồng khởi. Đúng súng của ta rồi! Việt muốn reo lên. Anh Tánh chắc ở đó, đơn vị mình ở đó. Chà, nổ dữ, phải chuẩn bị lựu đạn xung phong thôi! Đó, lại tiếng hụp hùm... chắc là một xe bọc thép vừa bị ta bắn cháy. Tiếng súng nghe thân thiết và vui lạ. Những khuôn mặt anh em mình lại hiện ra...Cái cằm nhọn hoắt ra của anh Tánh, nụ cười và cái nheo mắt của anh Công mỗi lần anh động viên Việt tiến lên...Việt vẫn còn đây, nguyên tại vị trí này, đạn đã lên nòng, ngón cái còn lại vẫn sẵn sàng nổ súng. Các anh chờ Việt một chút. Tiếng máy bay vẫn gầm rú hỗn loạn trên cao, nhưng mặc xác chúng. Kèn xung phong của chúng ta đã nổi lên. Lựu đạn ta đang nổ rộ...
(Những đứa con trong gia đình – Nguyễn Thi)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Văn hoá đọc là một khái niệm có hai nghĩa, một nghĩa rộng và một nghĩa hẹp. Ở nghĩa rộng, đó là ứng xử đọc, giá trị đọc và chuẩn mực đọc của mỗi cá nhân, của cộng đồng xã hội và của các nhà quản lí và cơ quan quản lí nhà nước. Như vậy, văn hoá đọc ở nghĩa rộng là sự hợp thành của ba yếu tố, hay chính xác hơn là ba lớp như ba vòng tròn không đồng tâm, ba vòng tròn giao nhau. Còn ở nghĩa hẹp, đó là ứng xử, giá trị và chuẩn mực đọc của mỗi cá nhân. Ứng xử, giá trị và chuẩn mực này cũng gồm ba thành phần: thói quen đọc, sở thích đọc và kĩ năng đọc. Ba thành phần này cũng là ba vòng tròn không đồng tâm, ba vòng tròn giao nhau.
Muốn phát triển nền văn hoá đọc phải phát triển ứng xử, giá trị và chuẩn mực đọc lành mạnh của các nhà quản lí và cơ quan quản lí nhà nước, của cộng đồng xã hội và của mỗi cá nhân trong xã hội. Nhưng trọng tâm và là mục đích cuối cùng của phát triển văn hoá đọc chính là phát triển ứng xử, giá trị và chuẩn mực đọc lành mạnh của mỗi thành viên trong xã hội. Ứng xử, giá trị và chuẩn mực đọc lành mạnh của mỗi cá nhân trong xã hội là thói quen đọc, sở thích đọc và kĩ năng đọc lành mạnh của họ. Đó chính là nền tảng của một xã hội học tập, của việc học suốt đời, một yêu cầu cũng là một thách thức của xã hội hiện đại.
Để hiểu sâu hơn về văn hoá đọc, chúng ta sẽ đi sâu vào từng nghĩa rộng và hẹp của khái niệm. Văn hoá đọc ở nghĩa rộng là ứng xử, giá trị và chuẩn mực đọc của các nhà quản lí và cơ quan quản lí nhà nước, ứng xử đọc của cộng đồng xã hội và ứng xử đọc của mỗi cá nhân trong xã hội.
Ứng xử, giá trị và chuẩn mực đọc của các nhà quản lí và cơ quan quản lí nhà nước là chính sách, đường lối và ứng xử hàng ngày nhằm phát triển nền văn hoá đọc. Các hoạt động này đều nhằm tạo ra hành lang pháp lí phát triển tài liệu đọc có giá trị và lành mạnh cho mọi người đọc khác nhau và sự thuận tiện của tài liệu đọc đến với người đọc (thông qua các loại cửa hàng sách và các loại hình thư viện, phòng đọc sách). Nghĩa là người đọc, không phân biệt giàu nghèo, không phân biệt tuổi tác, không phân biệt nơi cư trú đều dễ dàng tiếp cận đến những tài liệu đọc giá trị họ mong muốn, để họ có cơ hội cải thiện chính cuộc sống của họ.
(Văn hóa đọc và phát triển văn hóa đọc ở Việt Nam – Thư viện Quốc gia Việt Nam)
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Trước ngày 9 tháng 3, biết bao lần Việt Minh đã kêu gọi người Pháp liên minh để chống Nhật. Bọn thực dân Pháp đã không đáp ứng lại thẳng tay khủng bố Việt Minh hơn nữa. Thậm chí đến khi thua chạy, chúng còn nhẫn tâm giết nốt số đông tù chính trị ở Yên Bái và Cao Bằng.
Tuy vậy, đối với người Pháp, đồng bào ta vẫn giữ một thái độ khoan hồng và nhân đạo. Sau cuộc biến động ngày 9 tháng 3, Việt Minh đã giúp cho nhiều người Pháp chạy qua biên thùy, lại cứu cho nhiều người Pháp ra khỏi nhà giam Nhật và bảo vệ tính mạng và tài sản cho họ.
Sự thật là từ mùa thu năm 1940, nước ta đã thành thuộc địa của Nhật, chứ không phải thuộc địa của Pháp nữa. Khi Nhật hàng Đồng minh thì nhân dân cả nước ta đã nổi dậy giành chính quyền, lập nên nước Việt Nam Dân chủ Cộng hòa.
(Tuyên ngôn độc lập – Hồ Chí Minh)
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
…Ta đi ta nhớ những ngày
Mình đây ta đó, đắng cay ngọt bùi…
Thương nhau, chia củ sắn lùi
Bát cơm sẻ nửa, chăn sui đắp cùng.
Nhớ người mẹ nắng cháy lưng
Địu con lên rẫy, bẻ từng bắp ngô.
Nhớ sao lớp học i tờ
Đồng khuya đuốc sáng những giờ liên hoan
Nhớ sao ngày tháng cơ quan
Gian nan đời vẫn ca vang núi đèo.
Nhớ sao tiếng mõ rừng chiều
Chày đêm nện cối đều đều suối xa…
(Trích Việt Bắc – Tố Hữu)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Ngày 30-3-1972, quân ta mở cuộc Tiến công chiến lược đánh vào Quảng Trị, lấy Quảng Trị làm hướng tiến công chủ yếu, rồi phát triển rộng khắp chiến trường miền Nam.
Đến cuối tháng 6-1972, quân ta đã chọc thủng Ba phòng tuyến mạnh nhất của địch là Quảng Trị, Tây Nguyên, Đông Nam Bộ, loại khỏi vòng chiến đấu hơn 20 vạn quân Sài Gòn, giải phóng những vùng đất đai rộng lớn và đông dân.
Sau đòn mở đầu bất ngờ của quân ta, quân đội Sài Gòn có sự yểm trợ của Mĩ đã phản công, gây cho ta nhiều thiệt hại. Đế quốc Mĩ tiến hành trở lại cuộc chiến tranh phá hoại miền Bắc.
Cuộc Tiến công chiến lược năm 1972 đã giáng đòn nặng nề vào chiến lược "Việt Nam hoá chiến tranh", Buộc Mĩ phải tuyên bố "Mĩ hoá" trở lại chiến tranh xâm lược (tức thừa nhận sự thất bại của chiến lược "Việt Nam hoá chiến tranh")".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 183).
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.