Câu hỏi:
24/07/2024 134
Để xác định nồng độ dung dịch NaOH người ta tiến hành như sau: Cân 1,26 gam oxalic acid ngậm nước (\[{H_2}{C_2}{O_4}.2{H_2}O\]) hòa tan hoàn toàn vào nước, định mức thành 100 mL. Lấy 10 ml dung dịch này thêm vào đó vài giọt phenolphthalein, đem chuẩn độ bằng dung dịch NaOH đến xuất hiện màu hồng (ở pH = 9) thì hết 17,5 mL dung dịch NaOH. Tính nồng độ dung dịch NaOH đã dùng.
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
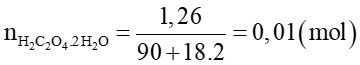
100 ml dung dịch oxalic acid chứa 0,01 mol \[{\left( {COOH} \right)_2}\]
10 ml ⟶ 0,001 mol
Đặt \[{n_{NaOH}} = {\rm{ }}x{\rm{ }}mol.\]
Phenolphthalein xuất hiện màu hồng ở pH = 9 > 7 ⟹ NaOH dư, \[{\left( {COOH} \right)_2}\]hết
Phương trình hóa học:
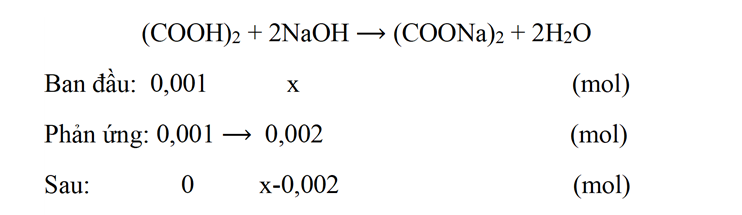
pH = 9 ⟹ pOH = 14 - 9 = 5 ⟹ \[{\left[ {O{H^ - }} \right]_{sau}} = {\rm{ }}{10^{ - 5}}\]
Ta có: \({[O{H^ - }]_{sau}} = \frac{{x - 0,002}}{{(10 + 17,5){{.10}^{ - 3}}}} = {10^{ - 5}}\)
\(\begin{array}{l} \Rightarrow x = 2,{000275.10^{ - 3}}\\ \Rightarrow {C_{M\,\,(NaOH)}} = \frac{{{n_{NaOH}}}}{{{V_{dd\,NaOH}}}} = \frac{{2,{{000275.10}^{ - 3}}}}{{17,{{5.10}^{ - 3}}}} = 0,1143\,M\end{array}\)
Chọn A.
Nhà sách vietjack
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian \[Oxyz,\] cho mặt phẳng \((\alpha ):ax - y + 2z + b = 0\) đi qua giao tuyến của hai mặt phẳng \((P):x - y - z + 1 = 0\) và \((Q):x + 2y + z - 1 = 0.\) Giá trị của \(a + 4b\) bằng
Xem đáp án »
25/06/2024
13,060
Câu 2:
Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + \left( {5 - m} \right)x\) đồng biến trên khoảng \(\left( {2\,;\,\, + \infty } \right)\) là
Xem đáp án »
25/06/2024
9,825
Câu 3:
Biết \(M\left( {1\,;\,\, - 5} \right)\) là một điểm cực trị của hàm số \(y = f\left( x \right) = a{x^3} + 4{x^2} + bx + 1.\) Giá trị \(f\left( 2 \right)\) bằng
Xem đáp án »
25/06/2024
8,179
Câu 4:
Gọi \(g\left( x \right)\) là một nguyên hàm của hàm số \[f\left( x \right) = \ln \left( {x - 1} \right).\] Cho biết \(g\left( 2 \right) = 1\) và \(g\left( 3 \right) = a\ln b\) trong đó \[a,\,\,b\] là các số nguyên dương phân biệt. Giá trị của \(T = 3{a^2} - {b^2}\) là
Xem đáp án »
25/06/2024
7,331
Câu 5:
Cho các số thực dương \(x \ne 1\,,\,\,y \ne 1\) thỏa mãn \({\log _2}x = {\log _y}16\) và tích \(xy = 64.\) Giá trị của biểu thức \({\left( {{{\log }_2}\frac{x}{y}} \right)^2}\) là
Xem đáp án »
25/06/2024
6,544
Câu 6:
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Xem đáp án »
11/07/2024
5,315
Câu 7:
Trên mặt phẳng tọa độ \[Oxy,\] cho điểm \(P\left( { - 3\,;\,\, - 2} \right)\) và đường tròn \(\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 36.\) Từ điểm \(P\) kẻ các tiếp tuyến \[PM\] và \[PN\] tới đường tròn \(\left( C \right),\) với \[M,\,\,N\] là các tiếp điểm. Phương trình đường thẳng \[MN\] là
Xem đáp án »
25/06/2024
3,718
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận