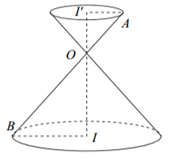
Cho một đồng hồ cát như bên dưới (gồm hai hình nón chung đỉnh ghép lại), trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc \(60^\circ .\) Biết rằng chiều cao của đồng hồ là \(30\;\,{\rm{cm}}\) và tổng thể tích của đồng hồ là \(1000\pi \,\,{\rm{c}}{{\rm{m}}^3}.\) Hỏi nếu cho đầy lượng cát vào phần bên trên thì khi chảy hết xuống dưới, tỉ số thể tích lượng cát chiếm chổ và thể tích phần phía dưới là bao nhiêu?

Trên giao tuyến \(\Delta \) của hai mặt phẳng \((P),\,\,(Q)\) ta lấy lần lượt 2 điểm \[A,\,\,B\] như sau:

• Lấy \(A\left( {x\,;\,\,y\,;\,\,1} \right) \in \Delta \), ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x - y = 0}\\{x + 2y = 0}\end{array} \Rightarrow x = y = 0 \Rightarrow A\left( {0\,;\,\,0\,;\,\,1} \right)} \right..\)

• Lấy \(B\left( { - 1\,;\,\,y\,;\,\,z} \right) \in \Delta \), ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{y + z = 0}\\{2y + z = 2}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2}\\{z =  - 2}\end{array} \Rightarrow B\left( { - 1\,;\,\,2\,;\,\, - 2} \right)} \right.} \right..\)

Vì \(\Delta  \in (\alpha )\) nên \(A,\,\,B \in (\alpha ).\) Do đó, ta có: \(\left\{ {\begin{array}{*{20}{l}}{2 + b = 0}\\{ - a + b - 6 = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a =  - 8}\\{b =  - 2}\end{array}} \right.} \right..\)

Vậy \(a + 4b =  - 8 + 4 \cdot \left( { - 2} \right) =  - 16.\) Chọn A.

Yêu cầu bài toán \( \Leftrightarrow f'\left( x \right) = 4m \cdot {x^3} + 16\left( {m - 6} \right)x \le 0\,;\,\,\forall x \in \left( {1\,;\,\,2} \right)\)

\( \Leftrightarrow 4x\left[ {m{x^2} + 4\left( {m - 6} \right)} \right] \le 0\,;\,\,\forall x \in \left( {1\,;\,\,2} \right)\)

\( \Leftrightarrow m{x^2} + 4m - 24 \le 0 \Leftrightarrow m\left( {{x^2} + 4} \right) \le 24 \Leftrightarrow m \le \frac{{24}}{{{x^2} + 4}}\,;\,\,\forall x \in \left( {1\,;\,\,2} \right)\)

\( \Leftrightarrow m \le {\min _{\left[ {1\,;\,\,2} \right]}}\left( {\frac{{24}}{{{x^2} + 4}}} \right) = 3\).

Mà \(m \in \left( { - 10\,;\,\,10} \right)\) suy ra có tất cả \(3 - \left( { - 9} \right) + 1 = 13\) giá trị nguyên của \(m\) cần tìm.

Chọn D.