Câu hỏi:
24/07/2024 41
Một khối thủy tinh được giữ trên bề mặt một chất lỏng chiết suất n. Tia sáng từ không khí tới bề mặt thủy tinh với góc tới 420, góc khúc xạ trong thủy tinh là 270 thì bắt đầu xảy ra hiện tượng phản xạ toàn phần tại bề mặt tiếp xúc giữa thủy tinh và chất lỏng (hình vẽ). Tính chiết suất của chất lỏng.
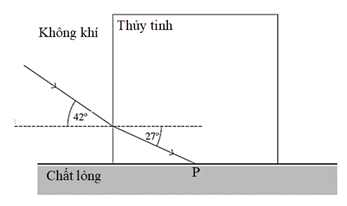
Một khối thủy tinh được giữ trên bề mặt một chất lỏng chiết suất n. Tia sáng từ không khí tới bề mặt thủy tinh với góc tới 420, góc khúc xạ trong thủy tinh là 270 thì bắt đầu xảy ra hiện tượng phản xạ toàn phần tại bề mặt tiếp xúc giữa thủy tinh và chất lỏng (hình vẽ). Tính chiết suất của chất lỏng.
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tại bề mặt tiếp xúc giữa thủy tinh và không khí, áp dụng công thức định luật khúc xạ ánh sáng, ta có: \(1.\sin i = {n_{tt}}.\sin r \Rightarrow 1.\sin 42^\circ = {n_{tt}}.\sin 27^\circ \Rightarrow {n_{tt}} \approx 1,47\)
Ta có: \(r + {i_1} = 90^\circ \Rightarrow {i_1} = 90^\circ - 27^\circ = 63^\circ \) (với i1 là góc tới tại P)
Tại bề mặt tiếp xúc giữa thủy tinh và chất lỏng bắt đầu xảy ra hiện tượng phản xạ toàn phần, ta có:
\(\sin {i_{gh}} = \frac{n}{{{n_{tt}}}} \Rightarrow \sin 63^\circ = \frac{n}{{1,47}} \Rightarrow n \approx 1,3\). Đáp án. 1,3
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số \(y = {x^3} - 3{x^2} + \left( {5 - m} \right)x\) đồng biến trên khoảng \(\left( {2\,;\,\, + \infty } \right)\) là
Xem đáp án »
25/06/2024
8,209
Câu 2:
Biết \(M\left( {1\,;\,\, - 5} \right)\) là một điểm cực trị của hàm số \(y = f\left( x \right) = a{x^3} + 4{x^2} + bx + 1.\) Giá trị \(f\left( 2 \right)\) bằng
Xem đáp án »
25/06/2024
6,484
Câu 3:
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Xem đáp án »
11/07/2024
4,234
Câu 4:
Trong không gian \[Oxyz,\] cho mặt phẳng \((\alpha ):ax - y + 2z + b = 0\) đi qua giao tuyến của hai mặt phẳng \((P):x - y - z + 1 = 0\) và \((Q):x + 2y + z - 1 = 0.\) Giá trị của \(a + 4b\) bằng
Xem đáp án »
25/06/2024
2,597
Câu 5:
Cho hàm số \(y = f\left( x \right) = {m^2}\left( {\sqrt {2 + x} + \sqrt {2 - x} } \right) + 4\sqrt {4 - {x^2}} + m + 1.\) Tổng tất cả các giá trị của \(m\) để hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng 4 là
Xem đáp án »
25/06/2024
1,824
Câu 6:
Cho hàm số \(y = \frac{{x + 3}}{{x + 1}}\) có đồ thị \[\left( C \right)\] và đường thẳng \(d:y = x - m\), với \(m\) là tham số thực. Biết rằng đường thẳng \(d\) cắt \[\left( C \right)\] tại hai điểm phân biệt \[A\] và \[B\] sao cho điểm \(G\left( {2\,;\,\, - 2} \right)\) là trọng tâm của tam giác \[OAB\] \[(O\] là gốc tọa độ). Giá trị của \(m\) bằng
Xem đáp án »
25/06/2024
1,722
Câu 7:
Ở các nước phát triển, lao động chủ yếu tập trung vào ngành nào sau đây?
Xem đáp án »
24/07/2024
1,093
về câu hỏi!