Một công ty có 50 căn phòng cho thuê. Biết rằng nếu công ty cho thuê mỗi căn phòng với giá 2 triệu đồng/1 tháng thì mọi căn phòng đều có người thuê, nhưng cứ mỗi lần tăng giá cho thuê mỗi căn phòng 100 000 đồng/1 tháng thì có thêm hai căn phòng bị bỏ trống. Công ty phải cho thuê mỗi căn phòng với giá là bao nhiêu để tổng số tiền thu được là lớn nhất?
Một công ty có 50 căn phòng cho thuê. Biết rằng nếu công ty cho thuê mỗi căn phòng với giá 2 triệu đồng/1 tháng thì mọi căn phòng đều có người thuê, nhưng cứ mỗi lần tăng giá cho thuê mỗi căn phòng 100 000 đồng/1 tháng thì có thêm hai căn phòng bị bỏ trống. Công ty phải cho thuê mỗi căn phòng với giá là bao nhiêu để tổng số tiền thu được là lớn nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đổi 100 000 đồng = 0,1 triệu đồng.
Gọi x là số lần tăng giá phòng (x ∈ ℕ*).
Số tiền tăng giá trong 1 tháng cho mỗi phòng là: 0,1x (triệu đồng).
Khi đó, giá cho thuê của mỗi căn phòng trong 1 tháng là: 2 + 0,1x (triệu đồng) và số phòng cho thuê được là: 50 – 2x.
Tổng số tiền thu được là: (2 + 0,1x)(50 – 2x) = 100 + x – 0,2x2 (triệu đồng).
Xét hàm số f(x) = 100 + x – 0,2x2, với 1 ≤ x ≤ 25.
Ta có: f’(x) = 1 – 0,4x.
f’(x) = 0 ⇔ x = 2,5.
Bảng biến thiên của hàm số:
|
x |
1 |
|
2,5 |
|
25 |
|
f’(x) |
|
+ |
0 |
– |
|
|
f(x) |
100,8 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có 
tại x = 2,5.
Vậy công ty phải cho thuê mỗi căn phòng với giá là 2 + 0,1.2,5 = 2,25 triệu đồng để tổng số tiền thu được là lớn nhất.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Xét hàm số G(x) = 0,025x2(30 – x) với 0 ≤ x ≤ 30.
Ta có: G’(x) = 0,025.[x2(30 – x)]’ = 0,025.(60x – 3x2) = 0,075x(20 – x).
Do đó G’(x) = 0 ⇔ x = 0 hoặc x = 20.
Bảng biến thiên của hàm số:
|
x |
0 |
|
20 |
|
30 |
|
G’(x) |
|
+ |
0 |
– |
|
|
G(x) |
0 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có 
tại x = 20.
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhanh nhất là 20 mg.
Lời giải
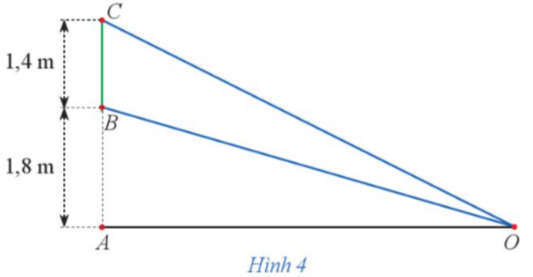
Cách 1. Để góc quan sát BOC là lớn nhất thì 
là nhỏ nhất.
Giả sử AO = x (m) (x > 0).
Suy ra 
và 
Ta có: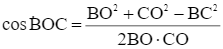 
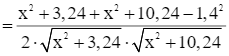
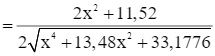
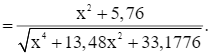
Xét hàm số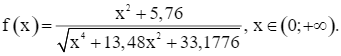 
Ta có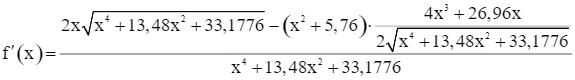 
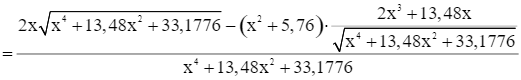
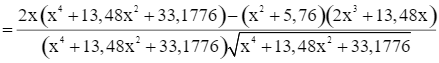
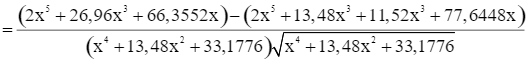
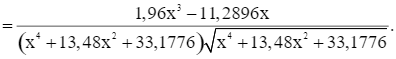
Do đó f’(x) = 0 ⇔ 1,96x3 – 11,2896x = 0 ⇔ x = 2,4 (vì x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
0,96 |
|
+∞
|
Căn cứ bảng biến thiên, ta có 
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Cách 2. Để góc quan sát BOC là lớn nhất thì 
là lớn nhất.
Giả sử AO = x (m) (x > 0).
Ta có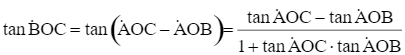 
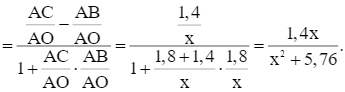
Xét hàm số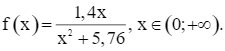 
Ta có: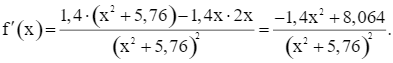 
Do đó f’(x) = 0 ⇔ x = 2,4 (do x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
|
|
+∞
|
Căn cứ bảng biến thiên, ta có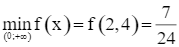 
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo