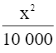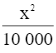Giải chuyên đề Toán 12 CD Bài 2. Vận dụng đạo hàm để giải quyết một số bài toán tối ưu trong thực tiễn có đáp án
40 người thi tuần này 4.6 679 lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Xét hàm số G(x) = 0,025x2(30 – x) với 0 ≤ x ≤ 30.
Ta có: G’(x) = 0,025.[x2(30 – x)]’ = 0,025.(60x – 3x2) = 0,075x(20 – x).
Do đó G’(x) = 0 ⇔ x = 0 hoặc x = 20.
Bảng biến thiên của hàm số:
|
x |
0 |
|
20 |
|
30 |
|
G’(x) |
|
+ |
0 |
– |
|
|
G(x) |
0 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có ![]() tại x = 20.
tại x = 20.
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhanh nhất là 20 mg.
Lời giải
Gọi chiều rộng của đáy hình hộp chữ nhật đó là x (m) (x > 0).
Chiều dài của đáy hình hộp chữ nhật đó là 2x (m).
Chiều cao của hình hộp chữ nhật đó là: 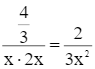 (m).
(m).
Diện tích đáy hình hộp chữ nhật đó là: x.2x = 2x2 (m2).
Diện tích xung quanh hình hộp chữ nhật đó là: 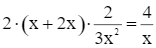 (m2).
(m2).
Diện tích tôn cần sử dụng là: 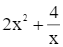 (m2).
(m2).
Xét hàm số 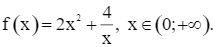
Ta có 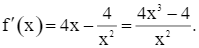
f’(x) = 0 ⇔ 4x3 – 4 = 0 ⇔ x = 1.
Bảng biến thiên của hàm số:
|
x |
0 |
|
1 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
6 |
|
+∞
|
Căn cứ bảng biến thiên, ta có ![]() tại x = 1.
tại x = 1.
Vậy chiều rộng của đáy hình hộp chữ nhật là 1 mét để số tôn cần sử dụng là nhỏ nhất.
Lời giải
Đổi 100 000 đồng = 0,1 triệu đồng.
Gọi x là số lần tăng giá phòng (x ∈ ℕ*).
Số tiền tăng giá trong 1 tháng cho mỗi phòng là: 0,1x (triệu đồng).
Khi đó, giá cho thuê của mỗi căn phòng trong 1 tháng là: 2 + 0,1x (triệu đồng) và số phòng cho thuê được là: 50 – 2x.
Tổng số tiền thu được là: (2 + 0,1x)(50 – 2x) = 100 + x – 0,2x2 (triệu đồng).
Xét hàm số f(x) = 100 + x – 0,2x2, với 1 ≤ x ≤ 25.
Ta có: f’(x) = 1 – 0,4x.
f’(x) = 0 ⇔ x = 2,5.
Bảng biến thiên của hàm số:
|
x |
1 |
|
2,5 |
|
25 |
|
f’(x) |
|
+ |
0 |
– |
|
|
f(x) |
100,8 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có ![]() tại x = 2,5.
tại x = 2,5.
Vậy công ty phải cho thuê mỗi căn phòng với giá là 2 + 0,1.2,5 = 2,25 triệu đồng để tổng số tiền thu được là lớn nhất.
Lời giải
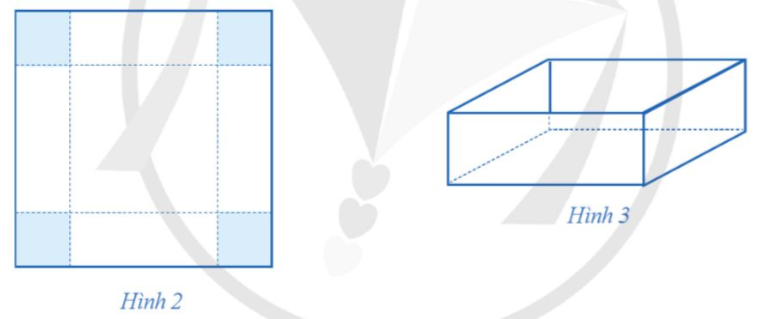
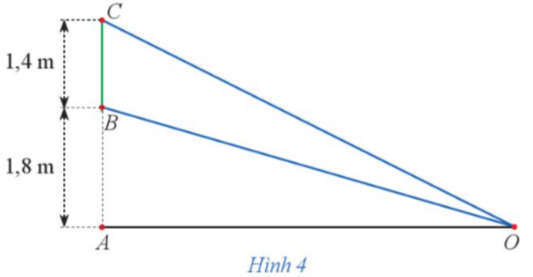
Cạnh đáy hình vuông của chiếc hộp không nắp là: 60 – 2x (cm).
Khi đó ta có: 60 – 2x < 37 hay x > 11,5.
Chiều cao của chiếc hộp không nắp là: x (cm). Khi đó ta có x < 28.
Diện tích đáy của chiếc hộp không nắp là: (60 – 2x)2 (cm2).
Thể tích của chiếc hộp không nắp là:
x.(60 – x)2 = x(3 600 – 240x + 4x2) = 3 600x – 240x2 + 4x3 (cm3).
Xét hàm số f(x) = 3 600x – 240x2 + 4x3 với 11,5 < x < 28.
Ta có f’(x) = 3 600 – 480x + 12x2.
Do đó f’(x) = 0 ⇔ x = 10 (thỏa mãn) hoặc x = 30 (không thỏa mãn).
Bảng biến thiên của hàm số:
|
x |
11,5 |
|
10 |
|
28 |
|
f’(x) |
|
+ |
0 |
– |
|
|
f(x) |
15 743,5 |
|
|
|
448 |
Căn cứ bảng biến thiên, ta có ![]() tại x = 10 (thỏa mãn điều kiện x là số nguyên dương).
tại x = 10 (thỏa mãn điều kiện x là số nguyên dương).
Vậy để làm được cái hộp đựng đồ có thể tích lớn nhất thì x = 10.
Lời giải
Cách 1. Để góc quan sát BOC là lớn nhất thì ![]() là nhỏ nhất.
là nhỏ nhất.
Giả sử AO = x (m) (x > 0).
Suy ra ![]() và
và ![]()
Ta có: 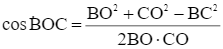
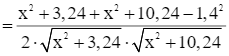
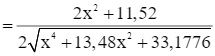
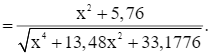
Xét hàm số 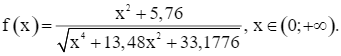
Ta có 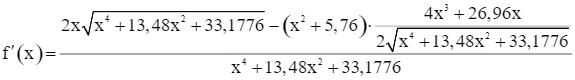
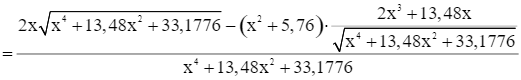
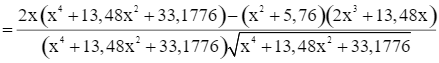
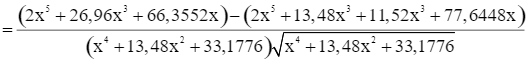
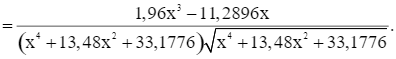
Do đó f’(x) = 0 ⇔ 1,96x3 – 11,2896x = 0 ⇔ x = 2,4 (vì x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
0,96 |
|
+∞
|
Căn cứ bảng biến thiên, ta có ![]() tại x = 2,4.
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Cách 2. Để góc quan sát BOC là lớn nhất thì ![]() là lớn nhất.
là lớn nhất.
Giả sử AO = x (m) (x > 0).
Ta có 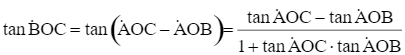
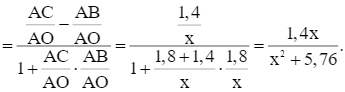
Xét hàm số 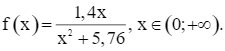
Ta có: 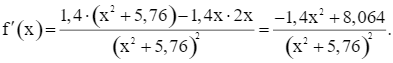
Do đó f’(x) = 0 ⇔ x = 2,4 (do x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
|
|
+∞
|
Căn cứ bảng biến thiên, ta có 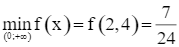 tại x = 2,4.
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.