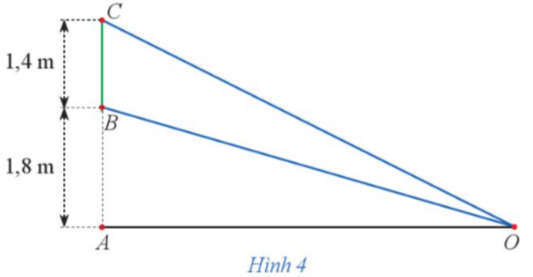
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn giá sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh bằng 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương x để làm được cái hộp đựng đồ có thể tích lớn nhất.
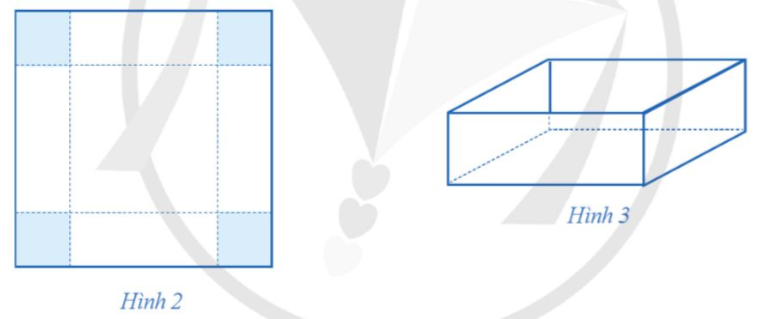
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn giá sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh bằng 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương x để làm được cái hộp đựng đồ có thể tích lớn nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cạnh đáy hình vuông của chiếc hộp không nắp là: 60 – 2x (cm).
Khi đó ta có: 60 – 2x < 37 hay x > 11,5.
Chiều cao của chiếc hộp không nắp là: x (cm). Khi đó ta có x < 28.
Diện tích đáy của chiếc hộp không nắp là: (60 – 2x)2 (cm2).
Thể tích của chiếc hộp không nắp là:
x.(60 – x)2 = x(3 600 – 240x + 4x2) = 3 600x – 240x2 + 4x3 (cm3).
Xét hàm số f(x) = 3 600x – 240x2 + 4x3 với 11,5 < x < 28.
Ta có f’(x) = 3 600 – 480x + 12x2.
Do đó f’(x) = 0 ⇔ x = 10 (thỏa mãn) hoặc x = 30 (không thỏa mãn).
Bảng biến thiên của hàm số:
|
x |
11,5 |
|
10 |
|
28 |
|
f’(x) |
|
+ |
0 |
– |
|
|
f(x) |
15 743,5 |
|
|
|
448 |
Căn cứ bảng biến thiên, ta có 
tại x = 10 (thỏa mãn điều kiện x là số nguyên dương).
Vậy để làm được cái hộp đựng đồ có thể tích lớn nhất thì x = 10.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Xét hàm số G(x) = 0,025x2(30 – x) với 0 ≤ x ≤ 30.
Ta có: G’(x) = 0,025.[x2(30 – x)]’ = 0,025.(60x – 3x2) = 0,075x(20 – x).
Do đó G’(x) = 0 ⇔ x = 0 hoặc x = 20.
Bảng biến thiên của hàm số:
|
x |
0 |
|
20 |
|
30 |
|
G’(x) |
|
+ |
0 |
– |
|
|
G(x) |
0 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có 
tại x = 20.
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhanh nhất là 20 mg.
Lời giải
Cách 1. Để góc quan sát BOC là lớn nhất thì 
là nhỏ nhất.
Giả sử AO = x (m) (x > 0).
Suy ra 
và 
Ta có: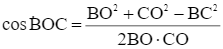 
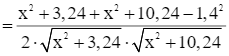
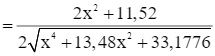
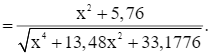
Xét hàm số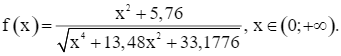 
Ta có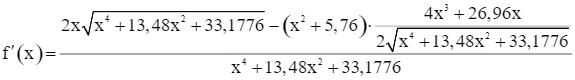 
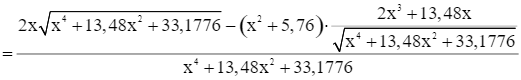
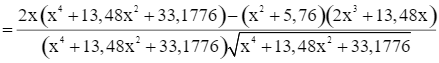
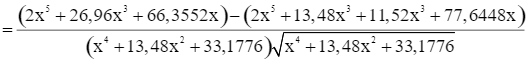
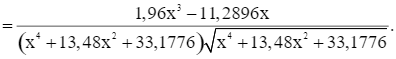
Do đó f’(x) = 0 ⇔ 1,96x3 – 11,2896x = 0 ⇔ x = 2,4 (vì x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
0,96 |
|
+∞
|
Căn cứ bảng biến thiên, ta có 
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Cách 2. Để góc quan sát BOC là lớn nhất thì 
là lớn nhất.
Giả sử AO = x (m) (x > 0).
Ta có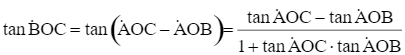 
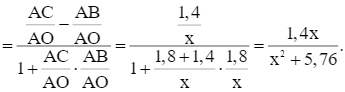
Xét hàm số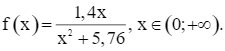 
Ta có: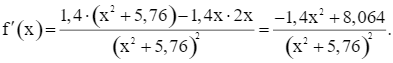 
Do đó f’(x) = 0 ⇔ x = 2,4 (do x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
|
|
+∞
|
Căn cứ bảng biến thiên, ta có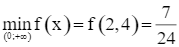 
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo