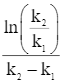Trong một phản ứng hoá học, lượng khí CO2 thoát ra V(t) được tính theo thời gian t bằng công thức:
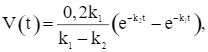
trong đó V(t) được tính theo đơn vị mililít và t được tính theo đơn vị giây; k1, k2 là các hằng số sao cho k1 > k2 > 0 (Nguồn: John W. Cell, Engineering Problems Illustrating Mathematics, McGraw-Hill Book Company, Inc. New York and London, 1943).
Lượng khí CO2 thoát ra trong phản ứng đó có giá trị lớn nhất là bao nhiêu?
Trong một phản ứng hoá học, lượng khí CO2 thoát ra V(t) được tính theo thời gian t bằng công thức:
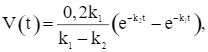
trong đó V(t) được tính theo đơn vị mililít và t được tính theo đơn vị giây; k1, k2 là các hằng số sao cho k1 > k2 > 0 (Nguồn: John W. Cell, Engineering Problems Illustrating Mathematics, McGraw-Hill Book Company, Inc. New York and London, 1943).
Lượng khí CO2 thoát ra trong phản ứng đó có giá trị lớn nhất là bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hàm số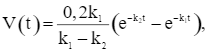 
với k1 > k2 > 0 và t ∈ (0; +∞).
Ta có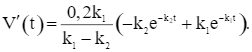 
Do đó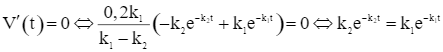 
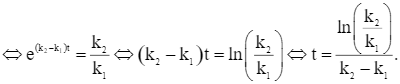
Đặt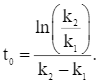 
Bảng biến thiên của hàm số:
|
t |
0 |
|
|
|
+∞ |
|
V’(t) |
|
+ |
0 |
– |
|
|
V(t) |
0 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có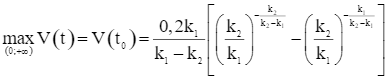 
tại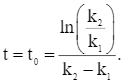 
Vậy lượng khí CO2 thoát ra trong phản ứng đó có giá trị lớn nhất là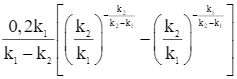 
(mililít).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Xét hàm số G(x) = 0,025x2(30 – x) với 0 ≤ x ≤ 30.
Ta có: G’(x) = 0,025.[x2(30 – x)]’ = 0,025.(60x – 3x2) = 0,075x(20 – x).
Do đó G’(x) = 0 ⇔ x = 0 hoặc x = 20.
Bảng biến thiên của hàm số:
|
x |
0 |
|
20 |
|
30 |
|
G’(x) |
|
+ |
0 |
– |
|
|
G(x) |
0 |
|
|
|
0 |
Căn cứ bảng biến thiên, ta có 
tại x = 20.
Vậy liều lượng thuốc cần tiêm cho bệnh nhân để huyết áp giảm nhanh nhất là 20 mg.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
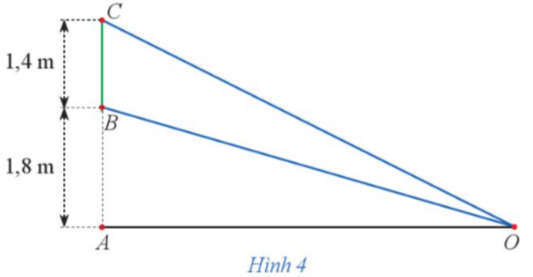
Cách 1. Để góc quan sát BOC là lớn nhất thì 
là nhỏ nhất.
Giả sử AO = x (m) (x > 0).
Suy ra 
và 
Ta có: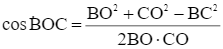 
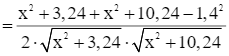
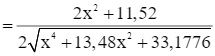
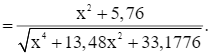
Xét hàm số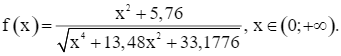 
Ta có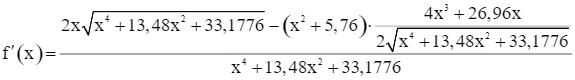 
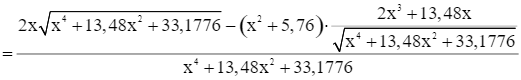
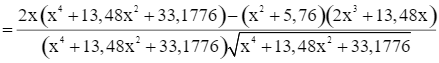
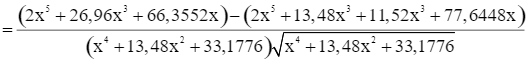
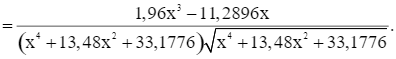
Do đó f’(x) = 0 ⇔ 1,96x3 – 11,2896x = 0 ⇔ x = 2,4 (vì x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
0,96 |
|
+∞
|
Căn cứ bảng biến thiên, ta có 
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Cách 2. Để góc quan sát BOC là lớn nhất thì 
là lớn nhất.
Giả sử AO = x (m) (x > 0).
Ta có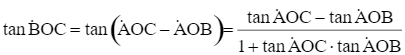 
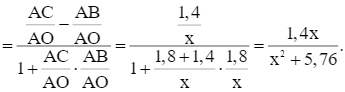
Xét hàm số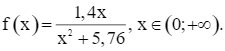 
Ta có: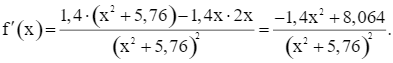 
Do đó f’(x) = 0 ⇔ x = 2,4 (do x > 0).
Bảng biến thiên của hàm số:
|
x |
0 |
|
2,4 |
|
+∞ |
|
f’(x) |
|
– |
0 |
+ |
|
|
f(x) |
|
|
|
|
+∞
|
Căn cứ bảng biến thiên, ta có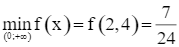 
tại x = 2,4.
Vậy để góc quan sát BOC là lớn nhất thì khoảng cách AO là 2,4 mét.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập