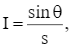Một vật nặng có khối lượng m được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc θ. Trong Vật lí, ta biết rằng lực kéo F cần thiết để di chuyển vật được cho bởi công thức
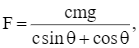
trong đó g là gia tốc trọng trường và c là hệ số ma sát của bề mặt (Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014). Chứng tỏ rằng lực kéo F nhỏ nhất khi tanθ = c.
Một vật nặng có khối lượng m được kéo dọc theo mặt phẳng nằm ngang nhờ một sợi dây hợp với phương ngang một góc θ. Trong Vật lí, ta biết rằng lực kéo F cần thiết để di chuyển vật được cho bởi công thức
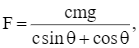
trong đó g là gia tốc trọng trường và c là hệ số ma sát của bề mặt (Theo Sullivan and Miranda, Calculus, W.H. Freeman and Company, 2014). Chứng tỏ rằng lực kéo F nhỏ nhất khi tanθ = c.
Câu hỏi trong đề: Giải SGK Chuyên đề Toán 12 Bài tập cuối chuyên đề 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hàm số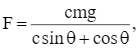 
với θ ∈ [0°; 90°].
Đạo hàm của hàm F là: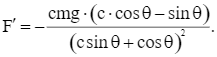 
Ta có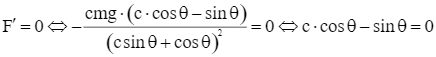 
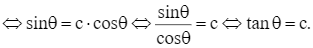
Giả sử θ0 thỏa mãn sao cho tanθ0 = c.
Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:
F(0°) = cmg;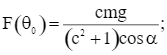 
F(90°) = mg.
Dễ thấy rằng F(α) là giá trị nhỏ nhất trong các giá trị F(0°), F(α), F(90°).
Do đó F đạt giá trị nhỏ nhất tại θ0 thỏa mãn tanθ0 = c.
Vậy lực kéo F nhỏ nhất khi tanθ = c.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
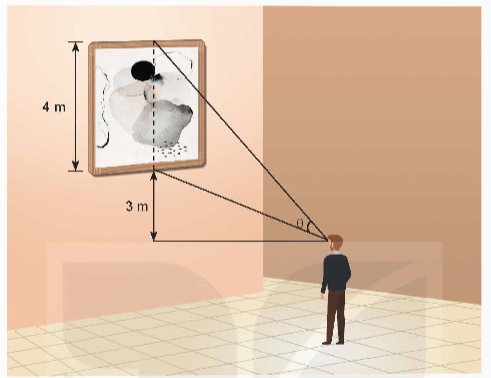
Giả sử tình huống được mô tả bởi hình vẽ dưới đây với C là vị trí mắt của người quan sát, DB = 4 m là chiều cao của bức tranh, AD = 3 m là khoảng cách từ mép dưới của bức tranh đến mắt người quan sát.
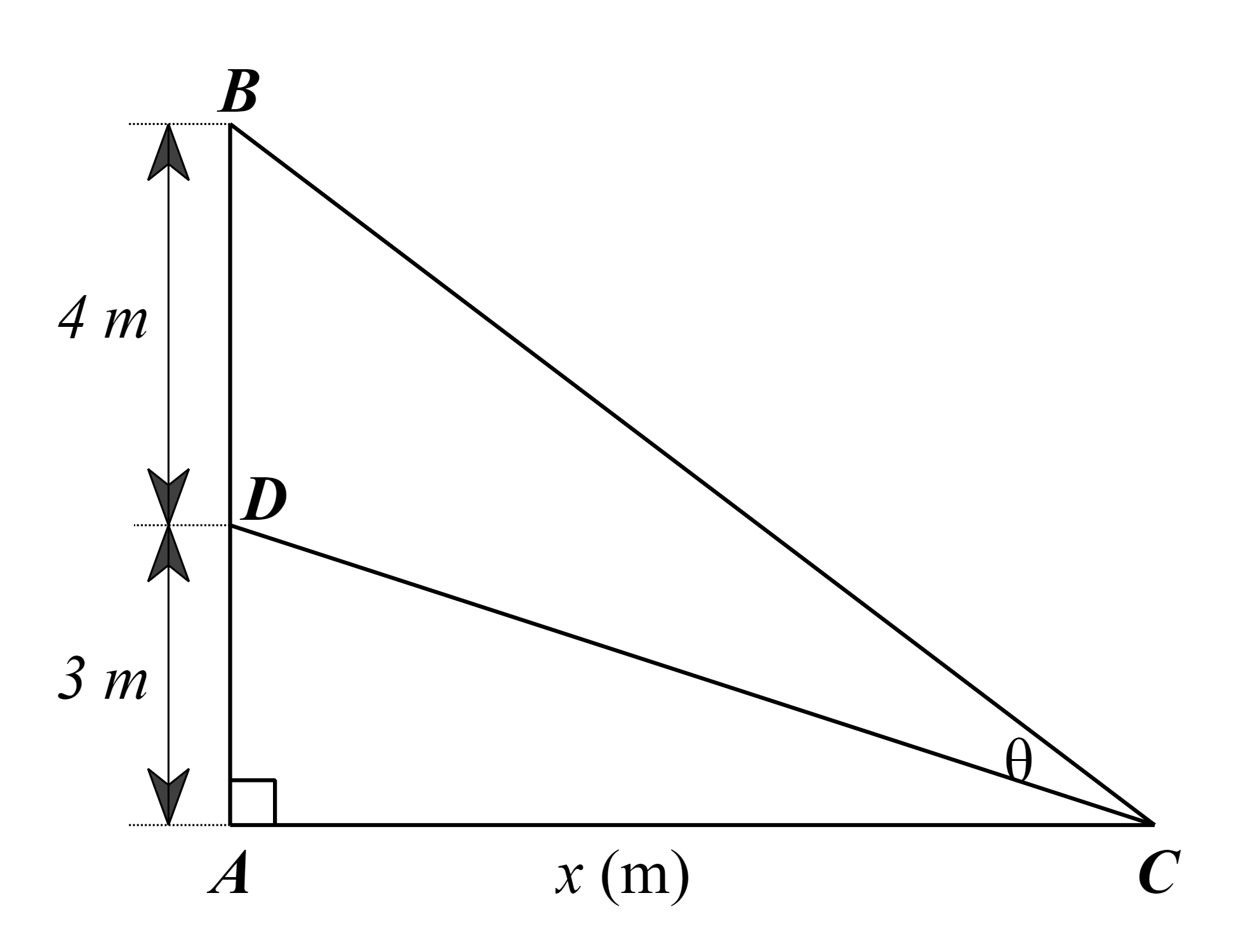
Giả sử AC = x (m) là khoảng cách từ người quan sát đến tường, x > 0.
Khi đó, ta có: 
và 
Áp dụng hệ quả định lí Cosin vào tam giác BCD, ta có:
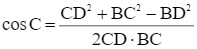
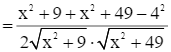
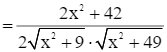
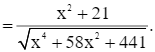
Hay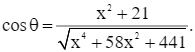 
Với θ ∈ (0°; 90°), để góc nhìn θ lớn nhất thì cosθ nhỏ nhất.
Đặt hàm số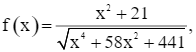 
xét trên khoảng (0; +∞).
Khi đó, ta cần tìm giá trị nhỏ nhất của f(x) trên (0; +∞).
Ta có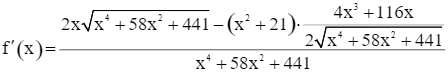 
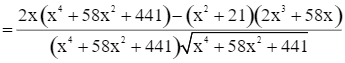
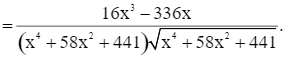
f’(x) = 0 ⇔ 16x3 – 336x = 0 ⇔ x = 0 (loại) hoặc x2 = 21
(do x ∈ (0; +∞)).
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).
|
|
0 |
|
|
|
+∞ |
|
|
|
– |
0 |
+ |
|
|
|
|
|
|
|
1
|
Từ bảng biến thiên, ta có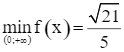 
khi 
Vậy người quan sát phải đứng cách tường 
mét để có được tầm nhìn thuận lợi nhất (tức là, có góc nhìn θ lớn nhất).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
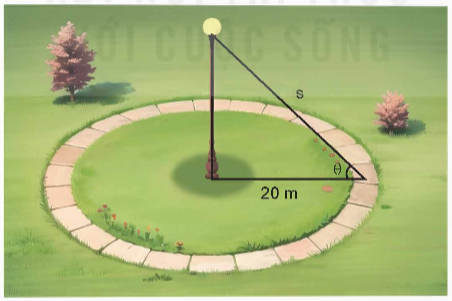
Gọi x (m) là chiều cao của đèn, x > 0.
Khi đó, ta có: s2 = x2 + 202 = x2 + 400 và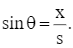 
Cường độ chiếu sáng của đèn là: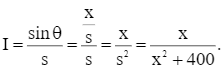 
Xét hàm số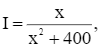 
trên khoảng (0; +∞).
Đạo hàm của hàm số I là: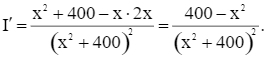 
Ta có I’ = 0 ⇔ 400 – x2 = 0 ⇔ x = 20 (do x > 0).
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).
|
|
0 |
|
20 |
|
+∞ |
|
|
|
+ |
0 |
– |
|
|
|
0 |
|
0,025
|
|
0 |
Từ bảng biến thiên, ta có 
khi x = 20.
Vậy độ cao của cột đèn là 20 mét thì sẽ chiếu sáng mạnh nhất cho lối đi bộ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập