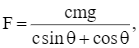Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở tâm của khu vực. Hỏi độ cao của cột đèn là bao nhiêu thì sẽ chiếu sáng mạnh nhất cho lối đi bộ? Biết rằng cường độ chiếu sáng được cho bởi công thức 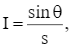 trong đó s là khoảng cách từ nguồn sáng và θ là góc mà ánh sáng chiếu vào bề mặt.
trong đó s là khoảng cách từ nguồn sáng và θ là góc mà ánh sáng chiếu vào bề mặt.
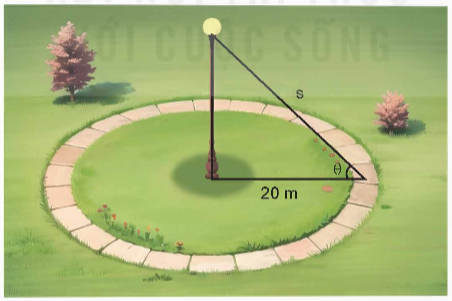
Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở tâm của khu vực. Hỏi độ cao của cột đèn là bao nhiêu thì sẽ chiếu sáng mạnh nhất cho lối đi bộ? Biết rằng cường độ chiếu sáng được cho bởi công thức 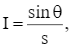 trong đó s là khoảng cách từ nguồn sáng và θ là góc mà ánh sáng chiếu vào bề mặt.
trong đó s là khoảng cách từ nguồn sáng và θ là góc mà ánh sáng chiếu vào bề mặt.

Quảng cáo
Trả lời:
Gọi x (m) là chiều cao của đèn, x > 0.
Khi đó, ta có: s2 = x2 + 202 = x2 + 400 và 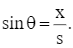
Cường độ chiếu sáng của đèn là: 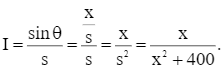
Xét hàm số 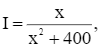 trên khoảng (0; +∞).
trên khoảng (0; +∞).
Đạo hàm của hàm số I là: 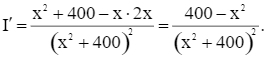
Ta có I’ = 0 ⇔ 400 – x2 = 0 ⇔ x = 20 (do x > 0).
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).
|
|
0 |
|
20 |
|
+∞ |
|
|
|
+ |
0 |
– |
|
|
|
0 |
|
0,025
|
|
0 |
Từ bảng biến thiên, ta có ![]() khi x = 20.
khi x = 20.
Vậy độ cao của cột đèn là 20 mét thì sẽ chiếu sáng mạnh nhất cho lối đi bộ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
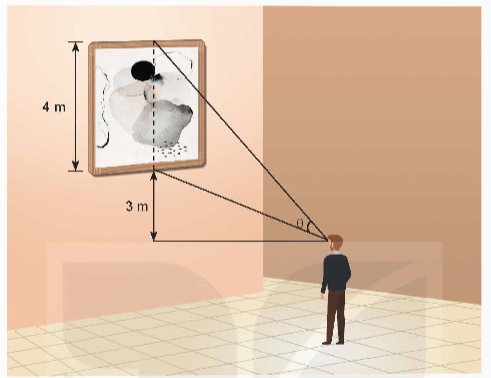
Giả sử tình huống được mô tả bởi hình vẽ dưới đây với C là vị trí mắt của người quan sát, DB = 4 m là chiều cao của bức tranh, AD = 3 m là khoảng cách từ mép dưới của bức tranh đến mắt người quan sát.
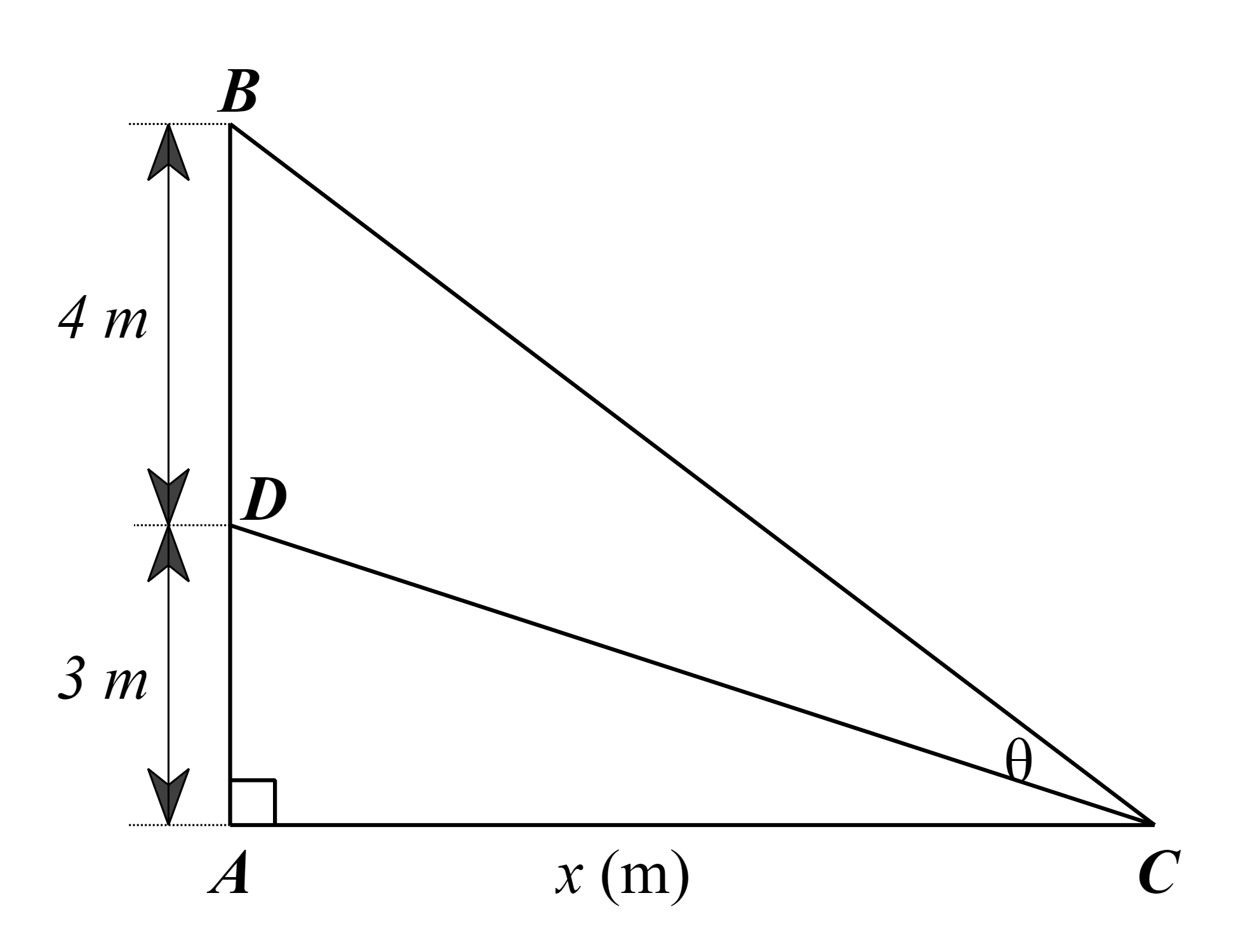
Giả sử AC = x (m) là khoảng cách từ người quan sát đến tường, x > 0.
Khi đó, ta có: ![]() và
và ![]()
Áp dụng hệ quả định lí Cosin vào tam giác BCD, ta có:
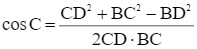
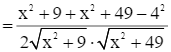
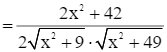
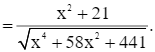
Hay 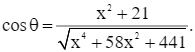
Với θ ∈ (0°; 90°), để góc nhìn θ lớn nhất thì cosθ nhỏ nhất.
Đặt hàm số 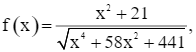 xét trên khoảng (0; +∞).
xét trên khoảng (0; +∞).
Khi đó, ta cần tìm giá trị nhỏ nhất của f(x) trên (0; +∞).
Ta có 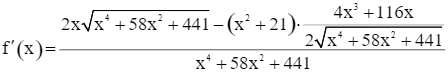
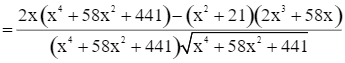
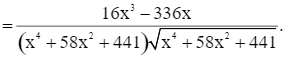
f’(x) = 0 ⇔ 16x3 – 336x = 0 ⇔ x = 0 (loại) hoặc x2 = 21
![]() (do x ∈ (0; +∞)).
(do x ∈ (0; +∞)).
Lập bảng biến thiên của hàm số trên khoảng (0; +∞).
|
|
0 |
|
|
|
+∞ |
|
|
|
– |
0 |
+ |
|
|
|
|
|
|
|
1
|
Từ bảng biến thiên, ta có 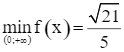 khi
khi ![]()
Vậy người quan sát phải đứng cách tường ![]() mét để có được tầm nhìn thuận lợi nhất (tức là, có góc nhìn θ lớn nhất).
mét để có được tầm nhìn thuận lợi nhất (tức là, có góc nhìn θ lớn nhất).
Lời giải
Gọi x và y lần lượt là số sản phẩm thứ nhất và sản phẩm thứ hai cần sản xuất.
Lợi nhuận thu được là: 400x + 600y (nghìn đồng).
Hệ bất phương trình ràng buộc x và y là
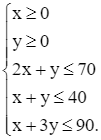
Miền nghiệm của hệ bất phương trình này là miền ngũ giác OABCD được tô màu như hình vẽ dưới đây:
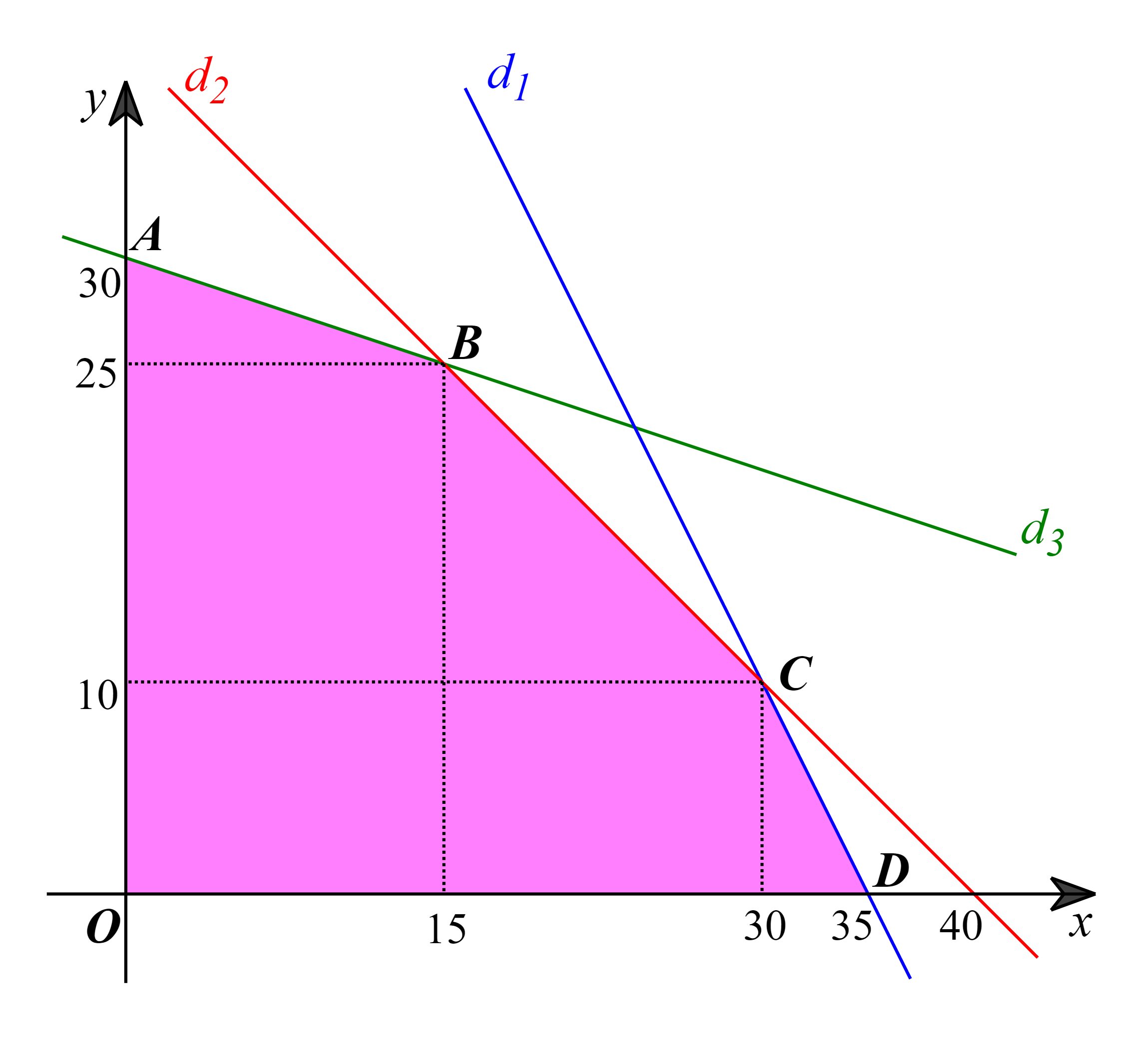
Ở đây, d1: 2x + y = 70, d2: x + y = 40 và d3: x + 3y = 90.
Các điểm cực biên là: O(0; 0), A(0; 30), B(15; 25), C(30; 10), D(35; 0).
Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác. Tính giá trị của F(x; y) tại các đỉnh của ngũ giác ta được:
F(0; 0) = 400.0 + 600.0 = 0;
F(0; 30) = 400.0 + 600.30 = 18 000;
F(15; 25) = 400.15 + 600.25 = 21 000;
F(30; 10) = 400.30 + 600.10 = 18 000;
F(35; 0) = 400.35 + 600.0 = 14 000.
Giá trị lớn nhất của F(x; y) bằng 21 000 tại điểm cực biên B(15; 25). Phương án tối ưu là (15; 25).
Vậy cần sản xuất 15 đơn vị sản phẩm thứ nhất và 25 đơn vị sản phẩm thứ hai để lợi nhuận thu được là lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.