Giải chuyên đề Toán 12 KNTT Bài tập cuối chuyên đề 2 có đáp án
42 người thi tuần này 4.6 448 lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Lời giải
Đổi 75 kg = 75 000 g; 120 kg = 120 000 g.
Hệ bất phương trình bậc nhất mô tả số lượng gói có thể có của mỗi loại là:
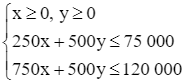 hay
hay 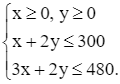
Lời giải
Miền nghiệm của hệ bất phương trình ở câu a là miền tứ giác OABC được tô màu như hình vẽ dưới đây:
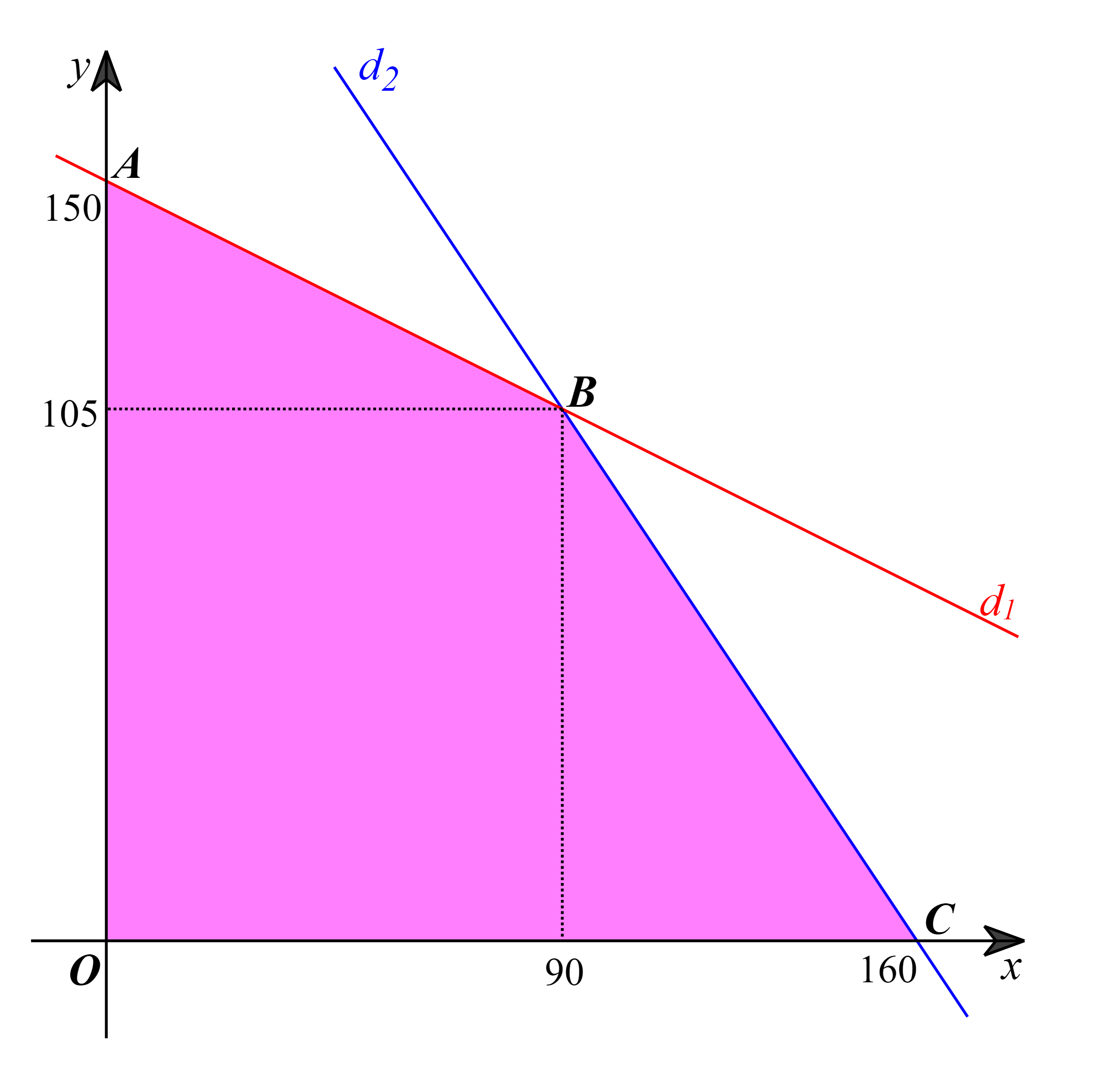
Ở đây, d1: x + 2y = 300 và d2: 3x + 2y = 480.
Các đỉnh của miền nghiệm là: O(0; 0), A(0; 150), B(90; 105), C(160; 0).
Lời giải
Lợi nhuận thu được là: F(x; y) = 30x + 40y (nghìn đồng).
Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các đỉnh của tứ giác ta được:
F(0; 0) = 30.0 + 40.0 = 0;
F(0; 150) = 30.0 + 40.150 = 6 000;
F(90; 105) = 30.90 + 40.105 = 6 900;
F(160; 0) = 30.160 + 40.0 = 4 800.
Giá trị lớn nhất của F(x; y) bằng 6 900 tại điểm cực biên B(90; 105). Phương án tối ưu là (90; 105).
Vậy cần chuẩn bị 90 gói cà phê tiêu chuẩn và 105 gói cà phê cao cấp để lợi nhuận thu được là lớn nhất.
Lời giải
Gọi x và y lần lượt là số sản phẩm thứ nhất và sản phẩm thứ hai cần sản xuất.
Lợi nhuận thu được là: 400x + 600y (nghìn đồng).
Hệ bất phương trình ràng buộc x và y là
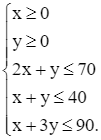
Miền nghiệm của hệ bất phương trình này là miền ngũ giác OABCD được tô màu như hình vẽ dưới đây:
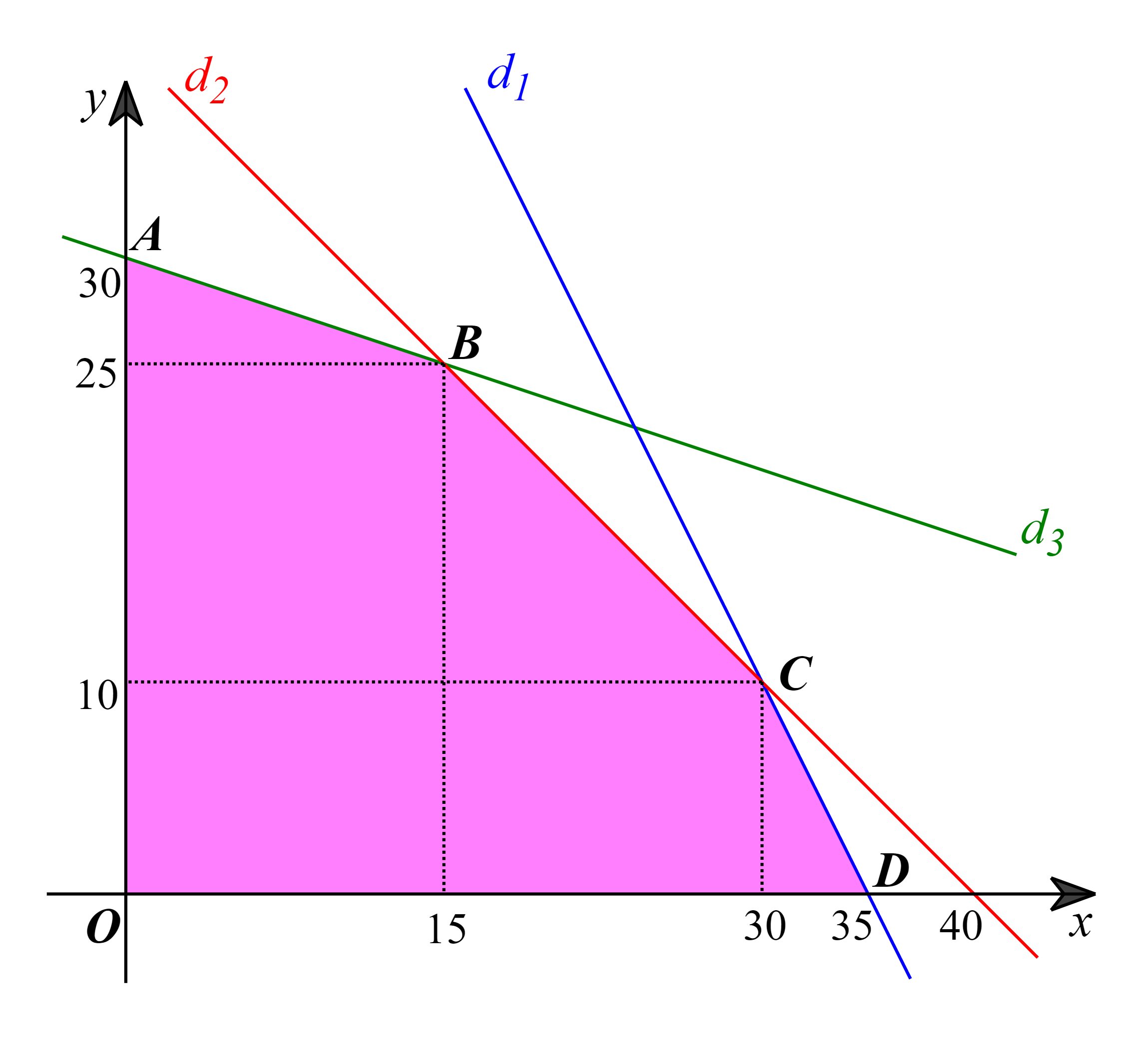
Ở đây, d1: 2x + y = 70, d2: x + y = 40 và d3: x + 3y = 90.
Các điểm cực biên là: O(0; 0), A(0; 30), B(15; 25), C(30; 10), D(35; 0).
Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác. Tính giá trị của F(x; y) tại các đỉnh của ngũ giác ta được:
F(0; 0) = 400.0 + 600.0 = 0;
F(0; 30) = 400.0 + 600.30 = 18 000;
F(15; 25) = 400.15 + 600.25 = 21 000;
F(30; 10) = 400.30 + 600.10 = 18 000;
F(35; 0) = 400.35 + 600.0 = 14 000.
Giá trị lớn nhất của F(x; y) bằng 21 000 tại điểm cực biên B(15; 25). Phương án tối ưu là (15; 25).
Vậy cần sản xuất 15 đơn vị sản phẩm thứ nhất và 25 đơn vị sản phẩm thứ hai để lợi nhuận thu được là lớn nhất.
Lời giải
Gọi x và y lần lượt là số đại diện bán hàng ở Hà Nội và Thành phố Hồ Chí Minh được cử đến dự cuộc họp bán hàng ở Đà Nẵng.
Tổng chi phí vé máy bay là: 2x + 2,4x (nghìn đồng).
Hệ bất phương trình ràng buộc x và y là
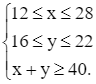
Miền nghiệm của hệ bất phương trình này là miền tứ giác ABCD được tô màu như hình vẽ dưới đây với đường thẳng d: x + y = 40.
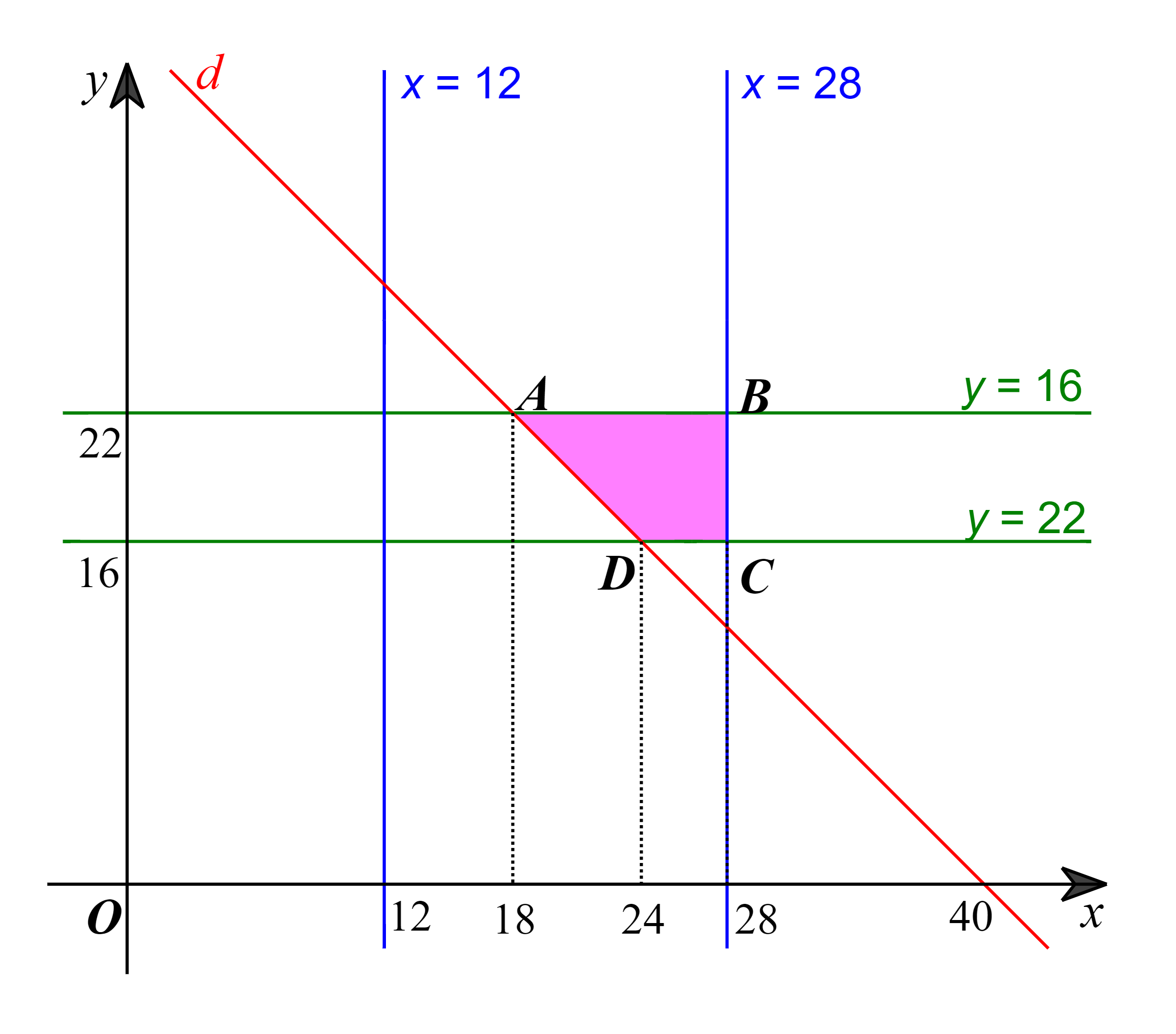
Các điểm cực biên là: A(18; 22), B(28; 22), C(28; 16), D(24; 16).
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các đỉnh của tứ giác ta được:
F(18; 22) = 2.18 + 2,4.22 = 88,8;
F(28; 22) = 2.28 + 2,4.22 = 108,8;
F(28; 16) = 2.28 + 2,4.16 = 94,4;
F(24; 16) = 2.24 + 2,4.16 = 86,4.
Giá trị nhỏ nhất của F(x; y) bằng 86,4 tại điểm cực biên B(24; 16). Phương án tối ưu là (24; 16).
Vậy cần cử 24 đại diện bán hàng ở Hà Nội và 16 đại diện bán hàng ở Thành phố Hồ Chí Minh đến dự cuộc họp bán hàng ở Đà Nẵng để tổng chi phí vé máy bay là nhỏ nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.