Trong lí thuyết tài chính, giá trị sổ sách là giá trị của một tài sản mà công ty sử dụng để xây dựng bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt tài sản.
Giả sử một công ty vừa mua một chiếc máy photocopy mới với giá 18 triệu đồng. Công ty lựa chọn cách tính khấu hao chiếc máy photocopy này theo phương pháp đường thẳng trong thời gian 3 năm, tức là mỗi năm giá trị của chiếc máy photocopy sẽ giảm 18 : 3 = 6 triệu đồng.
a) Viết hàm số bậc nhất biểu thị giá trị sổ sách V(x) của máy photocopy dưới dạng một hàm số theo thời gian sử dụng x (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất y = V(x).
c) Giá trị sổ sách của máy photocopy sau 2 năm sử dụng là bao nhiêu?
d) Sau thời gian sử dụng là bao lâu thì máy photocopy có giá trị sổ sách là 9 triệu đồng?
Trong lí thuyết tài chính, giá trị sổ sách là giá trị của một tài sản mà công ty sử dụng để xây dựng bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt tài sản.
Giả sử một công ty vừa mua một chiếc máy photocopy mới với giá 18 triệu đồng. Công ty lựa chọn cách tính khấu hao chiếc máy photocopy này theo phương pháp đường thẳng trong thời gian 3 năm, tức là mỗi năm giá trị của chiếc máy photocopy sẽ giảm 18 : 3 = 6 triệu đồng.
a) Viết hàm số bậc nhất biểu thị giá trị sổ sách V(x) của máy photocopy dưới dạng một hàm số theo thời gian sử dụng x (năm) của nó.
b) Vẽ đồ thị của hàm số bậc nhất y = V(x).
c) Giá trị sổ sách của máy photocopy sau 2 năm sử dụng là bao nhiêu?
d) Sau thời gian sử dụng là bao lâu thì máy photocopy có giá trị sổ sách là 9 triệu đồng?
Câu hỏi trong đề: Giải VTH Toán 8 KNTT Luyện tập chung trang 55 có đáp án !!
Quảng cáo
Trả lời:
a) Bảng giá trị sử dụng của máy photocopy là:
|
Đầu năm |
Hết năm 1 |
Hết năm 2 |
Hết năm 3 |
|
18 (triệu đồng) |
18 – 6 = 12 |
18 – 2.6 = 6 |
18 – 3.6 = 0 |
Hàm số bậc nhất biểu thị giá trị sổ sách V(x) của máy photocopy dưới dạng một hàm số theo thời gian sử dụng x (năm) của nó là V(x) = ax + b.
Dựa vào bảng trên, ta có:
Khi x = 2 thì y = 6, nghĩa là 6 = 2a + b. (1)
Khi x = 3 thì y = 0, nghĩa là 0 = 3a + b, hay b = −3a.
Thay b = −3a vào (1) suy ra 6 = 2a – 3a, hay a = −6, từ đó b = 18.
Vậy hàm số bậc nhất biểu thị giá trị sổ sách của máy photocopy là V(x) = −6x + 18.
b) Đồ thị của hàm số bậc nhất y = V(x) như hình bên.
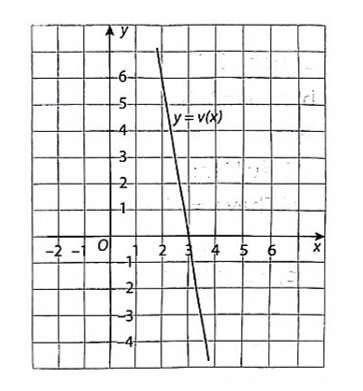
c) Thay x = 2 vào hàm số V(x), ta có:
V(2) = −6.2 + 18 = 6 (triệu đồng).
d) Để máy photocopy có giá trị sổ sách là 9 triệu đồng thì V(x) = 9, suy ra
9 = −6x + 18
6x = 9
x = 1,5
Vậy sau 1,5 năm sử dụng, giá trị sổ sách của chiếc máy photocopy sẽ là 9 triệu đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Hai đường thẳng đã cho song song với nhau khi m – 1 = −2 và m + 3 ≠ 1, hay m = −1 và m ≠ −2.
Suy ra m = −1. Giá trị này thỏa mãn điều kiện m ≠ 1.
Vậy giá trị m cần tìm là m = −1.
b) Với m = −1, ta có hàm số hàm số bậc nhất y = −2x + 2. Đồ thị hàm số như hình bên.
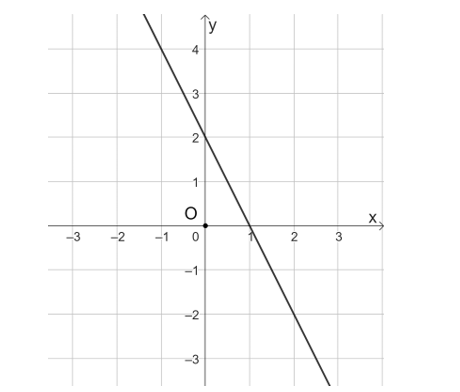
Lời giải
Điều kiện: m ≠ 3.
a) Đường thẳng đi qua điểm (1; 2) nên ta có:
2 = (3 – m).1 + 2m + 1, suy ra m = −2.
Giá trị này của m thỏa mãn điều kiện m ≠ 3. Vậy giá trị cần tìm là m = −2.
b) Vì đường thẳng y = x + 1 cắt trục tung tại điểm (0; 1), nên để đường thẳng đã cho cắt đường thẳng y = x + 1 tại một điểm nằm trên trục tung thì đường thẳng y = (3 – m)x + 2m + 1 phải đi qua điểm (0; 1). Từ đó suy ra
1 = (3 – m).0 + 2m + 1 hay m = 0.
So sánh với điều kiện của m ta thấy m = 0 thỏa mãn điều kiện.
Vậy giá trị cần tìm là m = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.