Giải VTH Toán 8 KNTT Luyện tập chung trang 55 có đáp án
36 người thi tuần này 4.6 329 lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 9
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Danh sách câu hỏi:
Lời giải
a) Đồ thị của hàm số y = 2 – 1 và y = −x + 2 như hình bên:
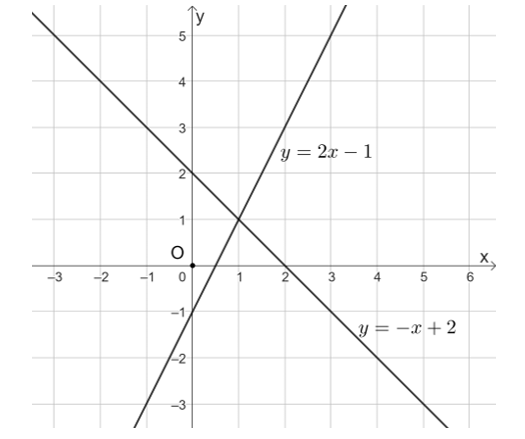
b) Gọi A(x0; y0) là giao điểm của hai đường thẳng đã cho.
Khi đó, cả hai đường thẳng đã cho đồng thời đi qua điểm A nên ta có: y0 = 2x0 – 1 và y0 = −x0 + 2, suy ra 2x0 – 1 = −x0 + 2, hay x0 = 1.
Do đó y0 = 1.
Vậy hai đường thẳng đã cho cắt nhau tại điểm A(1; 1).
Lời giải
Điều kiện: m ≠ 3.
a) Đường thẳng đi qua điểm (1; 2) nên ta có:
2 = (3 – m).1 + 2m + 1, suy ra m = −2.
Giá trị này của m thỏa mãn điều kiện m ≠ 3. Vậy giá trị cần tìm là m = −2.
b) Vì đường thẳng y = x + 1 cắt trục tung tại điểm (0; 1), nên để đường thẳng đã cho cắt đường thẳng y = x + 1 tại một điểm nằm trên trục tung thì đường thẳng y = (3 – m)x + 2m + 1 phải đi qua điểm (0; 1). Từ đó suy ra
1 = (3 – m).0 + 2m + 1 hay m = 0.
So sánh với điều kiện của m ta thấy m = 0 thỏa mãn điều kiện.
Vậy giá trị cần tìm là m = 0.
Lời giải
a) Hai đường thẳng đã cho song song với nhau khi m – 1 = −2 và m + 3 ≠ 1, hay m = −1 và m ≠ −2.
Suy ra m = −1. Giá trị này thỏa mãn điều kiện m ≠ 1.
Vậy giá trị m cần tìm là m = −1.
b) Với m = −1, ta có hàm số hàm số bậc nhất y = −2x + 2. Đồ thị hàm số như hình bên.
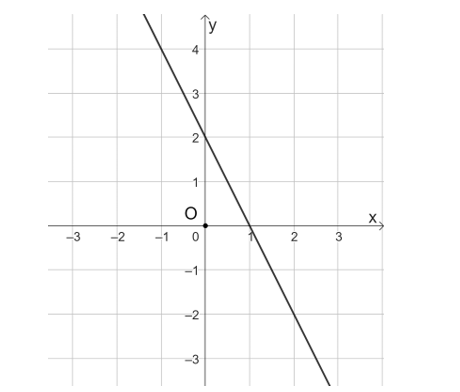
Lời giải
Giả sử hàm số bậc nhất cần tìm là y = ax + b (a ≠ 0).
Vì đường thẳng (d) song song với đồ thị hàm số (1) nên ta có a = 5.
Đường thẳng (d) cắt đồ thị hàm số (2) tại điểm A có hoành độ bằng 1 nên ta có tọa độ của A(1; −2). Khi đó, ta có: −2 = 5.1 + b, tức là b = −7.
Vậy hàm số cần tìm là y = 5x – 7.
Lời giải
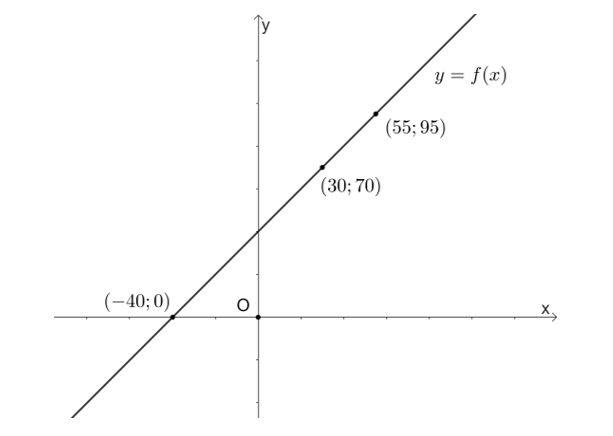
Từ đồ thị đã cho, ta có:
a) f(x) = 70 suy ra x = 30.
b) f(x) = 95 suy ra x = 55.
c) f(x) = 0 suy ra x = −40.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.