Cho hình chóp đều \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \(a\), cạnh bên hợp với đáy một góc bằng \(60^\circ .\) Kí hiệu \({V_1},\,\,{V_2}\) lần lượt là thể tích khối cầu ngoại tiếp, thể tích khối nón ngoại tiếp hình chóp đã cho. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng
Quảng cáo
Trả lời:
![Cho hình chóp đều \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \(a\), cạnh bên hợp với đáy một góc bằng \(60^\circ .\) Kí hiệu \({V_1},\,\,{V_2}\) l (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid9-1722384997.png)
Gọi \[O\] là tâm hình vuông \[ABCD.\] Suy ra \(SO \bot \left( {ABCD} \right).\)
Và góc giữa cạnh bên SA với mặt đáy \[\left( {ABCD} \right)\] là \(\widehat {SAO}.\)
Theo giả thiết \(\widehat {SAO} = 60^\circ \) nên \[\Delta SAC\] đều \( \Rightarrow SA = a\sqrt 2 \) và \(SO = \frac{{a\sqrt 6 }}{2}.\)
Gọi \(M\) là trung điểm \[SA.\] Trong \(\left( {SAC} \right)\), đường trung trực của cạnh \[SA\] cắt \[SO\] tại \[I.\]
Khi đó, \(I = IA = IB = IC = ID\) nên \(I\) là tâm của mặt cầu ngoại tiếp hình chóp \[S.ABCD.\]
Tam giác \[SAO\] có \(SI \cdot SO = SM \cdot SA \Rightarrow SI = \frac{{S{A^2}}}{{2SO}} = \frac{{a\sqrt 6 }}{3} = R.\)
Ta lại có, khối nón ngoại tiếp hình chóp có đường tròn đáy ngoại tiếp hình vuông \[ABCD\] nên có bán kính đáy \(r = \frac{{a\sqrt 2 }}{2}\) và chiều cao \(h = SO = \frac{{a\sqrt 6 }}{2}.\)
Suy ra \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{4}{3} \cdot \pi {{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^3}}}{{\frac{1}{3}\pi {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}\frac{{a\sqrt 6 }}{2}}} = \frac{{32}}{9}.\) Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Theo quyết định của Hội nghị lanta (2-1945), Đông Âu thuộc phạm vi ảnh hưởng của Liên Xô. Chọn C.
Câu 2
Lời giải
Ta có \(y = {x^3} - 3{x^2} \Rightarrow y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 2}\end{array}} \right..\)
Bảng biến thiên:
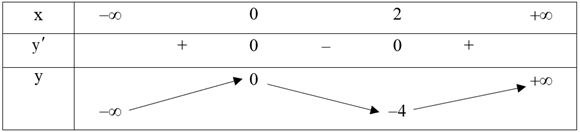
Dựa vào bảng biến thiên ta thấy đồ thị hàm số \(y = {x^3} - 3{x^2}\) cắt đường thẳng \(y = m\) tại ba điểm phân biệt khi \( - 4 < m < 0.\) Chọn B.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.