Câu hỏi:

02/08/2024 980

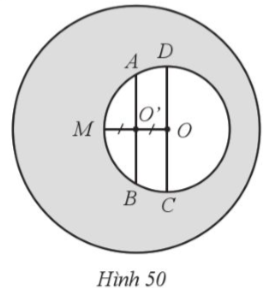
Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’, vuông góc với OM và đường kính CD song song với AB (Hình 50). Tính (làm tròn kết quả đến hàng đơn vị của centimét vuông):

a) Diện tích phần hình giới hạn bởi dây AB, cung nhỏ AD, đường kính CD và cung nhỏ BC của đường tròn (O);

b) Diện tích của phần tô màu xám.

Câu hỏi trong đề: Giải SBT Toán 9 Cánh Diều Bài 5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Xét ∆OAB cân tại O (do OA = OB) có OO’ là đường cao nên đồng thời là đường trung tuyến, đường phân giác của tam giác

Do OO’ là đường trung tuyến của ∆OAB nên O’ là trung điểm của AB, suy ra AB = 2AO’.

Do OO’ là đường phân giác của ∆OAB nên $\hat{A O M} = \hat{B O M},$ suy ra $\hat{A O D} = \hat{B O C} .$

Do O’ là trung điểm của OM nên $O O^{'} = \frac{1}{2} O M = \frac{1}{2} \cdot 8 = 4 (cm) .$

Xét ∆OO’A vuông tại O’, có:

⦁ $\cos \hat{A O O^{'}} = \frac{O O^{'}}{O A} = \frac{4}{8} = \frac{1}{2} .$

Suy ra $\hat{A O M} = 60 °,$ do đó $\hat{A O D} = \hat{B O C} = 30 ° .$

⦁ $A O^{'} = O A \cdot \sin \hat{A O O^{'}} = 8 \cdot \sin 60 ° = 8 \cdot \frac{\sqrt{3}}{2} = 4 \sqrt{3} (cm) .$

Diện tích tam giác OAB là: $S_{1} = \frac{1}{2} O O^{'} \cdot A B = \frac{1}{2} \cdot 4 \cdot 8 \sqrt{3} = 16 \sqrt{3} ({cm}^{2}) .$

Trong đường tròn (O), có $\hat{A O D} = \hat{B O C} = 30 °$ nên diện tích hình quạt tròn AOD và diện tích hình quạt tròn BOC bằng nhau và bằng: $S_{2} = \frac{π \cdot 8^{2} \cdot 30}{360} = \frac{16 π}{3} ({cm}^{2}) .$

Diện tích phần hình giới hạn bởi dây AB, cung nhỏ AD, đường kính CD và cung nhỏ BC của đường tròn (O) là: $S_{3} = S_{1} + 2 S_{2} = 16 \sqrt{3} + 2 \cdot \frac{16 π}{3} \approx 61 (c m^{2}) .$

b) Diện tích của phần tô màu xám bằng hiệu diện tích của hình tròn (O’) và hình tròn (O), và bằng:

π.16² ‒ π.8² =192π ≈ 603 (cm²).

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng 1,2 m, chiều dài 1,8 m và hai đầu là hai nửa hình tròn có đường kính là chiều rộng của hình chữ nhật như Hình 48. Tính số tiền bác Long phải trả để làm được mặt bàn đó (làm tròn kết quả đến hàng nghìn của đồng), biết giá gia công mỗi mét vuông mặt bàn là 100 000 đồng.

Xem đáp án

Lời giải

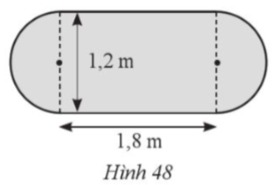
Diện tích mặt bàn là: 1,8.1,2 + π.0,6² = 2,16 + 0,36π (cm²).

Số tiền bác Long phải trả để làm được mặt bàn đó là:

100 000.(2,16 + 0,36π) ≈ 329 000 (đồng).

Câu 2

Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) và hai đầu là hai hình chữ nhật có chiều dài 15 cm, chiều rộng 5 cm. Tính diện tích mặt cắt của chi tiết máy ép nhựa đó (làm tròn kết quả đến hàng phần trăm của centimét vuông).

Xem đáp án

Lời giải

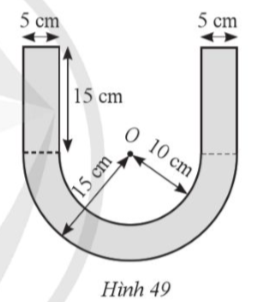
Diện tích mặt cắt của hai phần chi tiết có dạng hình chữ nhật là:

2 . (15 . 5) = 150 (cm²)

Diện tích của phần chi tiết có dạng nửa hình vành khuyên là: $\frac{1}{2} π \cdot (15^{2} - 10^{2}) = \frac{125}{2} π {(cm}^{2}) .$

Diện tích mặt cắt của chi tiết máy ép nhựa đó là: $150 + \frac{125}{2} π \approx 346, 35 ({cm}^{2}) .$

Câu 3

Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S₁ là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2 R), S₂ là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S₃ là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S₁ + S₂ = S₃.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A của hai đường tròn (O), (O’) (Hình 44).

Tính theo a:

a) Độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’);

b) Diện tích của phần tô màu xám theo a.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình chữ nhật ABCD với AB = 10 cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q. Biết rằng đường tròn tâm H đường kính PQ tiếp xúc với AB và CD (Hình 47). Tính diện tích phần chung của hai nửa đường tròn (O), (O’).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu