⦁ Diện tích của hình quạt tròn bán kính R, cung có số đo n° là $S = \frac{π R^{2} n}{360} = \frac{l R}{2},$ suy ra $n = \frac{360 S}{π R^{2}}$ và $l = \frac{2 S}{R} .$

Áp dụng các công thức trên, ta hoàn thành được bảng như sau:

Bán kính đường tròn (R)	Chu vi đường tròn (C)	Diện tích hình tròn (S)	Số đo của cung tròn (n^o)	Độ dài của cung tròn có số đo n^o	Diện tích của hình quạt tròn có số đo n^o
2 cm	12,56 cm	12,56 cm²	135°	4,71 cm	4,71 cm²
0,6 cm	3,768 cm	1,1304 cm²	120°	1,256 cm	0,3768 cm²
4 cm	25,12 cm	50,24 cm²	45°	3,14 cm	6,28 cm²
3 cm	18,84 cm	28,26 cm²	12°	0,628 cm	0,942 cm²

Câu 2

Chuyển động của Mặt Trăng quanh Trái Đất theo một quỹ đạo là gần giống đường tròn với tốc độ không đổi. Giả thiết quỹ đạo này là đường tròn với bán kính khoảng 385 nghìn km. Thời gian Mặt Trăng quay một vòng quanh Trái Đất khoảng 27,3 ngày.

a) Tính quãng đường đi được của Mặt Trăng sau 1 ngày (làm tròn kết quả đến hàng nghìn của kilômét).

b) Tính tốc độ của Mặt Trăng (làm tròn kết quả đến hàng đơn vị của mét trên giây).

Xem đáp án

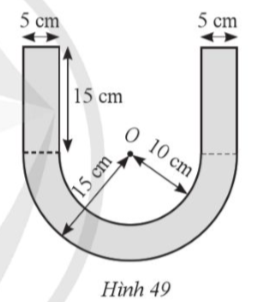
Lời giải

a) Quãng đường Mặt Trăng quay một vòng quanh Trái Đất chính là chu vi của đường tròn bán kính khoảng 385 nghìn km, và bằng: 2π . 385 000 = 770 000π (km).

Quãng đường đi được của Mặt Trăng sau 1 ngày khoảng: $\frac{770 000 π}{27, 3} \approx 89 000 (km) .$

b) Mặt Trăng đi được quãng đường khoảng 770 000π km sau 27,3 ngày nên ta có tốc độ của Mặt Trăng khoảng: $\frac{770 000 π \cdot 1000}{27, 3 \cdot 24 \cdot 60 \cdot 60} \approx 1 026 (m / s) .$

Câu 3

Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).

Xem đáp án

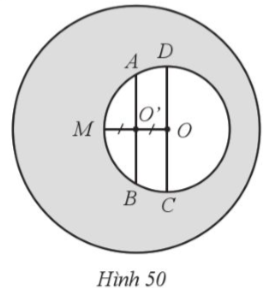
Lời giải

Media VietJack

Do ABCD là hình thoi nên $\hat{A} = \hat{C} .$ Đặt $\hat{A} = \hat{C} = n ° .$

Độ dài của cung nhỏ BD của đường tròn (A) là: $l_{1} = \frac{π \cdot 5 \cdot n}{180} (cm) .$

Độ dài của cung nhỏ EF của đường tròn (C) là: $l_{2} = \frac{π \cdot 3 \cdot n}{180} (cm) .$

Vậy tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C) là $\frac{l_{1}}{l_{2}} = \frac{π \cdot 5 \cdot n}{180} : \frac{π \cdot 3 \cdot n}{180} = \frac{5}{3} .$

Câu 4

Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A của hai đường tròn (O), (O’) (Hình 44).

Tính theo a:

a) Độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’);

b) Diện tích của phần tô màu xám theo a.

Xem đáp án

Lời giải

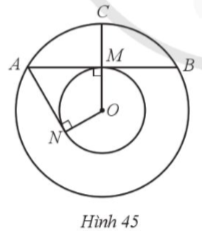
a) Ta có O, O’ lần lượt là trung điểm của AB, AE, mà AB = AE nên AO = AO’ = a.

Mà M là giao điểm của (O) và (O’) nên OM = OA và O’M = O’A.

Do đó OA = OM = O’A = O’M = a, nên AOMO’ là hình thoi

Lại có $\hat{O A O^{'}} = 90 °$ nên AOMO’ là hình vuông. Suy ra $\hat{A O M} = \hat{A O^{'} M} = 90 ° .$

Do đó, độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’) cùng bằng $\frac{π a \cdot 90}{180} = \frac{π a}{2} .$

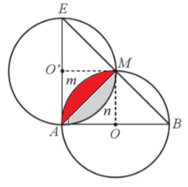
Media VietJack

Nối A với M. Khi đó diện tích của phần tô màu xám bằng 2 lần diện tích phần tô màu đỏ tạo bởi dây AM và cung AmM của đường tròn (O), và bằng 2 lần hiệu diện tích của hình quạt tròn bán kính a, cung có số đo 90° và diện tích tam giác OAM.

Diện tích của hình quạt tròn bán kính a, cung có số đo 90° là:

$\frac{π a^{2} \cdot 90}{360} = \frac{π a^{2}}{4}$ (đơn vị diện tích).

Diện tích của tam giác OAM là: $\frac{1}{2} O A \cdot O M = \frac{a^{2}}{2}$ (đơn vị diện tích).

Diện tích của phần tô màu đỏ là: $\frac{π a^{2}}{4} - \frac{a^{2}}{2} = \frac{(π - 2) a^{2}}{4}$ (đơn vị diện tích).

Vậy diện tích của phần tô màu xám là:

$2 \cdot \frac{(π - 2) a^{2}}{4} = \frac{(π - 2) a^{2}}{2}$ (đơn vị diện tích).

Câu 5

Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S₁ là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2 R), S₂ là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S₃ là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S₁ + S₂ = S₃.

Xem đáp án

Lời giải

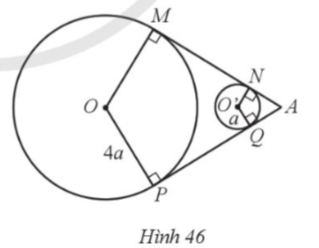
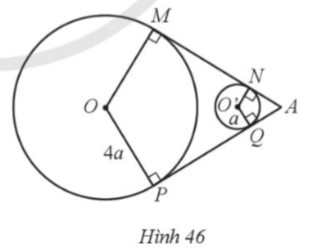
Do AM là tiếp tuyến của đường tròn (O; R) nên AM ⊥ OM tại M.

Xét tam giác OAM vuông tại M, theo định lí Pythagore, ta có:

OA² = OM² + AM²

Suy ra $A M = \sqrt{O A^{2} - O M^{2}}$ và $c o s \hat{A O M} = \frac{O M}{O A} = \frac{R}{2 R} = \frac{1}{2}$

Do đó $A M = \sqrt{{(2 R)}^{2} - R^{2}} = \sqrt{3 R^{2}} = R \sqrt{3}$ và $\hat{A O M} = 60 ° .$

Xét ∆OAM (vuông tại M) và ∆OBM (vuông tại M) có:

OA = OB, cạnh OM chung

Do đó ∆OAM = ∆OBM (cạnh huyền – cạnh góc vuông).

Suy ra $A M = B M = \frac{A B}{2}$ và $\hat{A O M} = \hat{B O M} = \frac{\hat{A O B}}{2} .$

Nên $A B = 2 A M = 2 R \sqrt{3}$ và $\hat{A O B} = 2 \hat{A O M} = 2 \cdot 60 ° = 120 ° .$

Do AM, AN là hai tiếp tuyến của đường tròn (O; R) nên OA là tia phân giác của góc MON, suy ra $\hat{M O N} = 2 \hat{A O M} = 2 \cdot 60 ° = 120 ° .$

Ta có:

⦁ S₁ = Diện tích hình quạt tròn AOB ‒ Diện tích tam giác OAB

Suy ra $S_{1} = \frac{π {(2 R)}^{2} \cdot 120}{360} - \frac{1}{2} \cdot R \cdot 2 R \sqrt{3} = R^{2} (\frac{4 π}{3} - \sqrt{3});$

⦁ S₂ = 2. Diện tích tam giác OAM ‒ Diện tích hình quạt tròn MON

Suy ra $S_{2} = 2 \cdot \frac{1}{2} \cdot R \cdot R \sqrt{3} - \frac{π R \cdot 120}{360} = R^{2} (\sqrt{3} - \frac{π}{3});$

⦁ S₃ = Diện tích hình tròn (O; R) = πR².

Khi đó $S_{1} + S_{2} = R^{2} (\frac{4 π}{3} - \sqrt{3}) + R^{2} (\sqrt{3} - \frac{π}{3})$

$= R^{2} (\frac{4 π}{3} - \sqrt{3} + \sqrt{3} - \frac{π}{3}) = π R^{2} = S_{3} .$

Vậy S₁ + S₂ = S₃.

Câu 6

Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A sao cho $\hat{M A P} = 60 °$ (Hình 46). Tìm độ dài của dây Curoa mắc qua hai ròng rọc theo a.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình chữ nhật ABCD với AB = 10 cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q. Biết rằng đường tròn tâm H đường kính PQ tiếp xúc với AB và CD (Hình 47). Tính diện tích phần chung của hai nửa đường tròn (O), (O’).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng 1,2 m, chiều dài 1,8 m và hai đầu là hai nửa hình tròn có đường kính là chiều rộng của hình chữ nhật như Hình 48. Tính số tiền bác Long phải trả để làm được mặt bàn đó (làm tròn kết quả đến hàng nghìn của đồng), biết giá gia công mỗi mét vuông mặt bàn là 100 000 đồng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) và hai đầu là hai hình chữ nhật có chiều dài 15 cm, chiều rộng 5 cm. Tính diện tích mặt cắt của chi tiết máy ép nhựa đó (làm tròn kết quả đến hàng phần trăm của centimét vuông).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’, vuông góc với OM và đường kính CD song song với AB (Hình 50). Tính (làm tròn kết quả đến hàng đơn vị của centimét vuông):

a) Diện tích phần hình giới hạn bởi dây AB, cung nhỏ AD, đường kính CD và cung nhỏ BC của đường tròn (O);

b) Diện tích của phần tô màu xám.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Giáo dục công dân

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học