✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

02/08/2024 937

Cho hình chữ nhật ABCD với AB = 10 cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q. Biết rằng đường tròn tâm H đường kính PQ tiếp xúc với AB và CD (Hình 47). Tính diện tích phần chung của hai nửa đường tròn (O), (O’).

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 9 Cánh Diều Bài 5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có $O P = O Q = \frac{A B}{2} = \frac{10}{2} = 5 (cm)$ và $O^{'} P = O^{'} Q = \frac{C D}{2}$

Mà AB = CD (do ABCD là hình chữ nhật) nên OP = OQ = O’P = O’Q = 5 cm.

Do đó POQO’ là hình thoi.

Mặt khác, đường tròn tâm H đường kính PQ tiếp xúc với AB tại O nên $\hat{P O Q}$ là góc nội tiếp chắn nửa đường tròn, do đó $\hat{P O Q} = 90 ° .$

Suy ra hình thoi POQO’ là hình vuông.

Diện tích hình quạt tròn POQ là: $S_{1} = \frac{π \cdot 5^{2} \cdot 90}{360} = \frac{25 π}{4} ({cm}^{2}) .$

Diện tích tam giác OPQ là:

$S_{2} = \frac{1}{2} \cdot$ Diện tích hình vuông POQO’ = $\frac{1}{2} \cdot 5^{2} = \frac{25}{2}$ (cm²).

Diện tích phần hình tạo bởi cung nhỏ PQ của đường tròn (O) và dây PQ là: $S_{3} = S_{1} - S_{2} = \frac{25}{4} (π - 2) ({cm}^{2}) .$

Diện tích phần chung của hai nửa đường tròn (O) và (O’) là: $S = 2 S_{3} = \frac{25}{2} (π - 2) ({cm}^{2}) .$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng 1,2 m, chiều dài 1,8 m và hai đầu là hai nửa hình tròn có đường kính là chiều rộng của hình chữ nhật như Hình 48. Tính số tiền bác Long phải trả để làm được mặt bàn đó (làm tròn kết quả đến hàng nghìn của đồng), biết giá gia công mỗi mét vuông mặt bàn là 100 000 đồng.

Xem đáp án

Lời giải

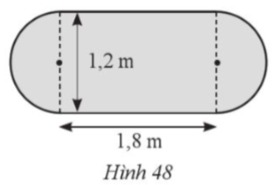
Diện tích mặt bàn là: 1,8.1,2 + π.0,6² = 2,16 + 0,36π (cm²).

Số tiền bác Long phải trả để làm được mặt bàn đó là:

100 000.(2,16 + 0,36π) ≈ 329 000 (đồng).

Câu 2

Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) và hai đầu là hai hình chữ nhật có chiều dài 15 cm, chiều rộng 5 cm. Tính diện tích mặt cắt của chi tiết máy ép nhựa đó (làm tròn kết quả đến hàng phần trăm của centimét vuông).

Xem đáp án

Lời giải

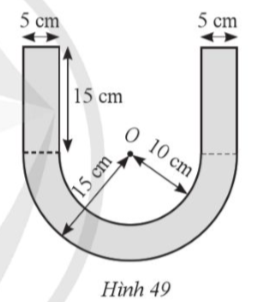
Diện tích mặt cắt của hai phần chi tiết có dạng hình chữ nhật là:

2 . (15 . 5) = 150 (cm²)

Diện tích của phần chi tiết có dạng nửa hình vành khuyên là: $\frac{1}{2} π \cdot (15^{2} - 10^{2}) = \frac{125}{2} π {(cm}^{2}) .$

Diện tích mặt cắt của chi tiết máy ép nhựa đó là: $150 + \frac{125}{2} π \approx 346, 35 ({cm}^{2}) .$

Câu 3

Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F. Tính tỉ số độ dài của cung nhỏ BD của đường tròn (A) và cung nhỏ EF của đường tròn (C).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S₁ là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2 R), S₂ là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S₃ là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S₁ + S₂ = S₃.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A của hai đường tròn (O), (O’) (Hình 44).

Tính theo a:

a) Độ dài cung AmM và cung AnM tương ứng của đường tròn (O) và (O’);

b) Diện tích của phần tô màu xám theo a.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’, vuông góc với OM và đường kính CD song song với AB (Hình 50). Tính (làm tròn kết quả đến hàng đơn vị của centimét vuông):

a) Diện tích phần hình giới hạn bởi dây AB, cung nhỏ AD, đường kính CD và cung nhỏ BC của đường tròn (O);

b) Diện tích của phần tô màu xám.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »