Câu hỏi:
08/08/2024 124
Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định gắn chung tại một điểm O. Con lắc (I) nằm ngang trên mặt bàn nhẵn. Con lắc (II) treo thẳng đứng cạnh mép bàn như hình vẽ. Kích thích cho hai con lắc dao động điều hòa tự do. Chọn mốc thế năng đàn hồi của mỗi con lắc tại các vị trí tương ứng của vật lúc lò xo có chiều dài tự nhiên. Thế năng đàn hồi các con lắc phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ.
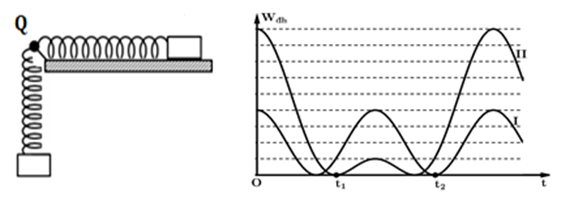
Biết tại thời điểm t = 0, cả hai lò xo đều dãn và \({t_2} - {t_1} = \frac{{\rm{\pi }}}{{12}}\;{\rm{s}}{\rm{.}}\) Lấy \({\rm{g}} = 10\;\)m/s2. Tại thời điểm \({\rm{t}} = \frac{{\rm{\pi }}}{{10}}\;{\rm{s}}\), khoảng cách hai vật dao động mạch có giá trị bằng bao nhiêu cm? Làm tròn đến số thập phân thứ nhất.
Đáp án: ……….
Hai con lắc lò xo cấu tạo giống nhau, có cùng chiều dài tự nhiên bằng 80 cm và đầu cố định gắn chung tại một điểm O. Con lắc (I) nằm ngang trên mặt bàn nhẵn. Con lắc (II) treo thẳng đứng cạnh mép bàn như hình vẽ. Kích thích cho hai con lắc dao động điều hòa tự do. Chọn mốc thế năng đàn hồi của mỗi con lắc tại các vị trí tương ứng của vật lúc lò xo có chiều dài tự nhiên. Thế năng đàn hồi các con lắc phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ.
Biết tại thời điểm t = 0, cả hai lò xo đều dãn và \({t_2} - {t_1} = \frac{{\rm{\pi }}}{{12}}\;{\rm{s}}{\rm{.}}\) Lấy \({\rm{g}} = 10\;\)m/s2. Tại thời điểm \({\rm{t}} = \frac{{\rm{\pi }}}{{10}}\;{\rm{s}}\), khoảng cách hai vật dao động mạch có giá trị bằng bao nhiêu cm? Làm tròn đến số thập phân thứ nhất.
Đáp án: ……….
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có hình vẽ, chọn hệ quy chiếu như hình vẽ:
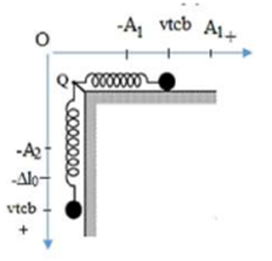
Đường (I) cho biết thế năng đàn hồi của con lắc lò xo nằm ngang.
Thế năng cực đại ứng với 4 đơn vị: \({{\rm{W}}_1} = \frac{1}{2}{\rm{kA}}_1^2\).
Đường (II) là thế năng đàn hồi của con lắc lò xo treo thẳng đứng. Vì tại vị trí cân bằng lò xo đã dãn một đoạn \(\Delta {\ell _0}\) nên tại vị trí lò xo dãn nhiều nhất, thế năng đàn hồi cực đại lớn nhất ứng với 9 đơn vị: \({{\rm{W}}_{2 + }} = \frac{1}{2}{\rm{k}}{\left( {{\rm{A}} + \Delta {\ell _0}} \right)^2}\)
Tại vị trí biên trên (biên âm) thì thế năng đàn hồi ứng với 1 đơn vị: \({{\rm{W}}_{2 - }} = \frac{1}{2}{\rm{k}}{\left( {{\rm{A}} - \Delta {\ell _0}} \right)^2}\)
Ta có tỉ số: \(\left\{ \begin{array}{l}\frac{{{{\rm{W}}_{2 + }}}}{{{{\rm{W}}_{2 - }}}} = \frac{9}{1} = \frac{{{{\left( {{{\rm{A}}_2} + \Delta {\ell _0}} \right)}^2}}}{{{{\left( {\;{{\rm{A}}_2} - \Delta {\ell _0}} \right)}^2}}} \Leftrightarrow \frac{{\left( {{{\rm{A}}_2} + \Delta {\ell _0}} \right)}}{{\left( {{{\rm{A}}_2} - \Delta {\ell _0}} \right)}} = 3 \Rightarrow {{\rm{A}}_2} = 2\Delta {\ell _0}\\\frac{{{{\rm{W}}_{2 + }}}}{{{{\rm{W}}_1}}} = \frac{9}{4} = \frac{{{{\left( {{{\rm{A}}_2} + \Delta {\ell _0}} \right)}^2}}}{{\;{\rm{A}}_1^2}} \Leftrightarrow \frac{{{{\rm{A}}_2} + \Delta {\ell _0}}}{{\;{{\rm{A}}_1}}} = \frac{3}{2} \Leftrightarrow \frac{{3\Delta {\ell _0}}}{{\;{{\rm{A}}_1}}} = \frac{3}{2} \Rightarrow {{\rm{A}}_1} = 2\Delta {\ell _0} = {{\rm{A}}_2}\end{array} \right.\)
Tại thời điểm ban đầu \(t = 0\), ta thấy cả hai vật đều đang ở biên dương. Thời điểm \({t_1}\) là thời điểm vật của lò xo treo thẳng đứng đi qua vị trí lò xo không dãn.
Thời gian từ \({\rm{t}} = 0\) đến \({{\rm{t}}_1}\) là \({{\rm{t}}_1} = \frac{{\rm{T}}}{3}\)
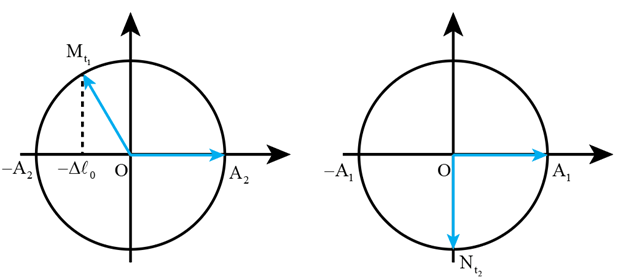
Thời điểm \({t_2}\) là thời điểm vật của lò xo nằm ngang đi qua vị trí cân bằng lần thứ 2. Thời gian từ \({\rm{t}} = 0\) đến \({{\rm{t}}_2}\) là \({{\rm{t}}_2} = \frac{3}{4}\;{\rm{T}}\).
Khoảng thời gian \({{\rm{t}}_2} - {{\rm{t}}_1} = \frac{{\rm{\pi }}}{{12}} \Rightarrow \frac{3}{4}\;{\rm{T}} - \frac{{\rm{T}}}{3} = \frac{5}{{12}}\;{\rm{T}} = \frac{{\rm{\pi }}}{{12}} \Rightarrow {\rm{T}} = \frac{{\rm{\pi }}}{5}(\;{\rm{s}})\)
Tần số góc của hai con lắc là như nhau vì chúng đều dao động tự do và có cùng độ cứng, vật nặng cùng khối lượng:
\({\rm{\omega }} = \sqrt {\frac{{\rm{k}}}{{\rm{m}}}} = \sqrt {\frac{{\rm{g}}}{{\Delta {\ell _0}}}} \Rightarrow {\rm{\omega }} = \frac{{2{\rm{\pi }}}}{{\rm{T}}} = \frac{{2{\rm{\pi }}}}{{\frac{{\rm{\pi }}}{5}}} = 10 = \sqrt {\frac{{\rm{g}}}{{\Delta {\ell _0}}}} \Rightarrow \Delta {\ell _0} = 0,1\;{\rm{m}} = 10\;{\rm{cm}} \Rightarrow {{\rm{A}}_1} = {{\rm{A}}_2} = 20\;{\rm{cm}}.\)
Sau thời gian \({\rm{t}} = {\rm{t}} = \frac{{\rm{\pi }}}{{10}}\;{\rm{s}} = \frac{{\rm{T}}}{2}\) thì hai vật đều đang ở biên âm.
Khoảng cách giữa hai vật lúc này là:
\({\rm{d}} = \sqrt {{{\left( {\ell - {{\rm{A}}_1}} \right)}^2} + {{\left( {\ell + \Delta {\ell _0} - {{\rm{A}}_2}} \right)}^2}} = \sqrt {{{(80 - 20)}^2} + {{(80 + 10 - 20)}^2}} = 92,2\;{\rm{cm}}{\rm{. }}\)Đáp án. 92,2
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm số \(f\left( x \right)\) có đúng một điểm cực trị khi và chỉ khi tam thức \(g\left( x \right) = {x^2} + 2mx + 5\) vô nghiệm hoặc có hai nghiệm phân biệt trong đó một nghiệm là \(x = - 1\), hoặc \(g\left( x \right)\) có nghiệm kép.
Tức là \(\left[ {\begin{array}{*{20}{l}}{{{\Delta '}_g} < 0}\\{\left\{ {\begin{array}{*{20}{l}}{g( - 1) = 0}\\{\Delta ' > 0}\end{array}} \right.}\\{{{\Delta '}_g} = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 5 < 0}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2m + 6 = 0}\\{{m^2} - 5 > 0}\end{array}} \right.}\\{{m^2} - 5 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - \sqrt 5 \le m \le \sqrt 5 }\\{m = 3}\end{array}} \right.} \right.} \right..\)
Do đó tập các giá trị nguyên thỏa mãn yêu cầu bài toán là \(S = \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3} \right\}.\)
Đáp án: 6.
Lời giải
Năm 2021 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot \left( {1 - 0,02} \right) = 850 \cdot 0,98\) (triệu đồng).
Năm 2022 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^2}\) (triệu đồng).
Năm 2023 hãng xe ô tô niêm yết giá bán xe X là: \[850 \cdot 0,{98^3}\] (triệu đồng).
Năm 2024 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^4}\) (triệu đồng).
Năm 2025 hãng xe ô tô niêm yết giá bán xe X là:
\(850 \cdot 0,{98^5} = 768,3326 \approx 768,333\) (triệu đồng).
Vậy 2025 hãng xe ô tô niêm yết giá bán xe X là \[768\,\,333\,\,000\] đồng. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận