Câu hỏi:
08/08/2024 115
Điện phân dung dịch hỗn hợp \({\rm{NaCl}}\) và 0,05 mol \({\rm{CuS}}{{\rm{O}}_4}\) bằng dòng điện một chiều có cường độ 2A (điện cực trơ, có màng ngăn). Sau thời gian t giây thì ngừng điện phân thu được khí ở hai điện cực có tổng thể tích là 2,85 lít (đkc) và dung dịch X. Dung dịch X hòa tan được tối đa 1,02 gam \({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}.\) Giả sử hiệu suất điện phân là 100%, các khí thoát ra không tan trong dung dịch. Giá trị của t là
Đáp án: ……….
Điện phân dung dịch hỗn hợp \({\rm{NaCl}}\) và 0,05 mol \({\rm{CuS}}{{\rm{O}}_4}\) bằng dòng điện một chiều có cường độ 2A (điện cực trơ, có màng ngăn). Sau thời gian t giây thì ngừng điện phân thu được khí ở hai điện cực có tổng thể tích là 2,85 lít (đkc) và dung dịch X. Dung dịch X hòa tan được tối đa 1,02 gam \({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}.\) Giả sử hiệu suất điện phân là 100%, các khí thoát ra không tan trong dung dịch. Giá trị của t là
Đáp án: ……….
Quảng cáo
Trả lời:
Giải bởi Vietjack
\({{\rm{n}}_{{\rm{CuS}}{{\rm{O}}_4}}} = 0,05\,(\;{\rm{mol}}),{{\rm{n}}_{{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}} = 0,01\,(\;{\rm{mol}}),\,{n_{kh\'i }} = \frac{{2,85}}{{24,79}} = 0,115\,(mol)\)
TH1: Giả sử \({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\) bị hòa tan là do \({\rm{O}}{{\rm{H}}^ - }\)
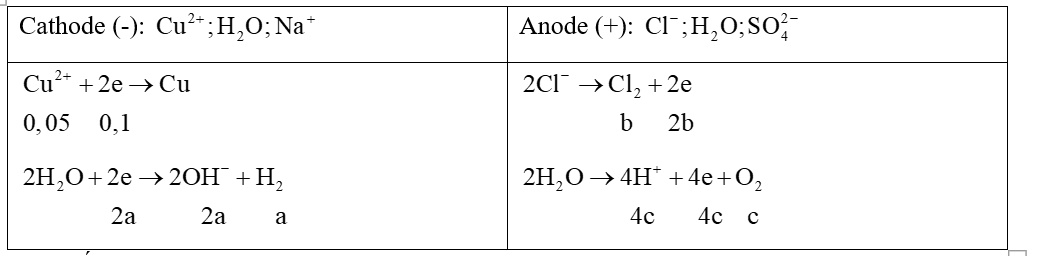
Ta có số mol khí ở hai điện cực: \({\rm{a}} + {\rm{b}} + {\rm{c}} = 0,115\) (1)
Bảo toàn electron: \(0,1 + 2{\rm{a}} = 2\;{\rm{b}} + 4{\rm{c}}\) (2)
\(\begin{array}{l}2O{H^ - } + A{l_2}{O_3} \to 2AlO_2^ - + {H_2}O\\0,02 \leftarrow 0,01\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(mol)\end{array}\)
\({{\rm{n}}_{{\rm{O}}{{\rm{H}}^ - }}} = 2{{\rm{n}}_{{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}}} = 0,02 = 2{\rm{a}} - 4{\rm{c}}\) (3)
Từ (1), (2), (3) \( \Rightarrow {\rm{a}} = 0,04;{\rm{b}} = 0,06;{\rm{c}} = 0,015.\)
\({{\rm{n}}_{\rm{c}}} = \frac{{{\rm{It}}}}{{\rm{F}}} \Rightarrow 0,1 + 2 \cdot 0,04 = \frac{{5{\rm{t}}}}{{96500}} \Rightarrow {\rm{t}} = 3474\;{\rm{s}}{\rm{.}}\)
TH2: Giả sử \({\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3}\) bị hòa tan là do \({H^ + }\)
Làm tương tự và chỉ ra TH2 không thể xảy ra.
Đáp án: 3474
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm số \(f\left( x \right)\) có đúng một điểm cực trị khi và chỉ khi tam thức \(g\left( x \right) = {x^2} + 2mx + 5\) vô nghiệm hoặc có hai nghiệm phân biệt trong đó một nghiệm là \(x = - 1\), hoặc \(g\left( x \right)\) có nghiệm kép.
Tức là \(\left[ {\begin{array}{*{20}{l}}{{{\Delta '}_g} < 0}\\{\left\{ {\begin{array}{*{20}{l}}{g( - 1) = 0}\\{\Delta ' > 0}\end{array}} \right.}\\{{{\Delta '}_g} = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 5 < 0}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2m + 6 = 0}\\{{m^2} - 5 > 0}\end{array}} \right.}\\{{m^2} - 5 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - \sqrt 5 \le m \le \sqrt 5 }\\{m = 3}\end{array}} \right.} \right.} \right..\)
Do đó tập các giá trị nguyên thỏa mãn yêu cầu bài toán là \(S = \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3} \right\}.\)
Đáp án: 6.
Lời giải
Năm 2021 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot \left( {1 - 0,02} \right) = 850 \cdot 0,98\) (triệu đồng).
Năm 2022 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^2}\) (triệu đồng).
Năm 2023 hãng xe ô tô niêm yết giá bán xe X là: \[850 \cdot 0,{98^3}\] (triệu đồng).
Năm 2024 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^4}\) (triệu đồng).
Năm 2025 hãng xe ô tô niêm yết giá bán xe X là:
\(850 \cdot 0,{98^5} = 768,3326 \approx 768,333\) (triệu đồng).
Vậy 2025 hãng xe ô tô niêm yết giá bán xe X là \[768\,\,333\,\,000\] đồng. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận