Câu hỏi:
08/08/2024 197
Sơ đồ phả hệ dưới đây mô tả sự di truyền bệnh mù màu và bệnh máu khó đông ở người.
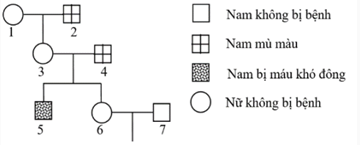
Mỗi bệnh do 1 trong 2 alen của 1 gen nằm ở vùng không tương đồng trên NST giới tính X quy định, 2 gen này cách nhau 20 cM. Theo lí thuyết, xác suất sinh con bị cả 2 bệnh của cặp 6 - 7 là bao nhiêu? (làm tròn đến số thập phân thứ 2).
Đáp án: ……….
Sơ đồ phả hệ dưới đây mô tả sự di truyền bệnh mù màu và bệnh máu khó đông ở người.
Mỗi bệnh do 1 trong 2 alen của 1 gen nằm ở vùng không tương đồng trên NST giới tính X quy định, 2 gen này cách nhau 20 cM. Theo lí thuyết, xác suất sinh con bị cả 2 bệnh của cặp 6 - 7 là bao nhiêu? (làm tròn đến số thập phân thứ 2).
Đáp án: ……….
Quảng cáo
Trả lời:
Giải bởi Vietjack
. - Bệnh mù màu và bệnh máu khó đông đều do gen lặn nằm trên NST giới tính X quy định → Quy ước gen: A - bình thường >> a - bị mù màu; B - bình thường >> b - bị máu khó đông.
- Hai gen này cách nhau 20 cM → Xảy ra hiện tượng hoán vị gen với tần số 20%.
- Xác định kiểu gen của từng người trong phả hệ:
+ Người số 3 sinh con trai (5) bị máu khó đông nên phải có\(X_b^A\) và nhận\(X_B^a\)của bố (2) nên có kiểu gen là \(X_b^AX_B^a\).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
(A-, Bb) |
\(X_B^aY\) |
\(X_b^AX_B^a\) |
\(X_B^aY\) |
\(X_b^AY\) |
\(X_ - ^AX_B^a\) |
\(X_B^AY\) |
+ Để cặp (6) - (7) sinh con bị 2 bệnh thì kiểu gen của người (6) phải là \(X_b^AX_B^a\) với xác suất 0,8 (Người số (6) bình thường nhận\(X_B^a\)của bố (4) và có mẹ (3) có kiểu gen\(X_b^AX_B^a\)với tần số hoán vị 20% nên xác suất kiểu gen của người (6) là 0,1\(X_B^AX_B^a\): 0,4\(X_b^AX_B^a\)).
Vậy cặp (6) - (7): \(0,8X_b^AX_B^a \times X_B^AY \to X_b^aY = 0,8 \times 0,1X_b^a \times 0,5Y = 0,04.\) Đáp án: 0,04.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm số \(f\left( x \right)\) có đúng một điểm cực trị khi và chỉ khi tam thức \(g\left( x \right) = {x^2} + 2mx + 5\) vô nghiệm hoặc có hai nghiệm phân biệt trong đó một nghiệm là \(x = - 1\), hoặc \(g\left( x \right)\) có nghiệm kép.
Tức là \(\left[ {\begin{array}{*{20}{l}}{{{\Delta '}_g} < 0}\\{\left\{ {\begin{array}{*{20}{l}}{g( - 1) = 0}\\{\Delta ' > 0}\end{array}} \right.}\\{{{\Delta '}_g} = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m^2} - 5 < 0}\\{\left\{ {\begin{array}{*{20}{c}}{ - 2m + 6 = 0}\\{{m^2} - 5 > 0}\end{array}} \right.}\\{{m^2} - 5 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - \sqrt 5 \le m \le \sqrt 5 }\\{m = 3}\end{array}} \right.} \right.} \right..\)
Do đó tập các giá trị nguyên thỏa mãn yêu cầu bài toán là \(S = \left\{ { - 2\,;\,\, - 1\,;\,\,0\,;\,\,1\,;\,\,2\,;\,\,3} \right\}.\)
Đáp án: 6.
Lời giải
Năm 2021 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot \left( {1 - 0,02} \right) = 850 \cdot 0,98\) (triệu đồng).
Năm 2022 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^2}\) (triệu đồng).
Năm 2023 hãng xe ô tô niêm yết giá bán xe X là: \[850 \cdot 0,{98^3}\] (triệu đồng).
Năm 2024 hãng xe ô tô niêm yết giá bán xe X là: \(850 \cdot 0,{98^4}\) (triệu đồng).
Năm 2025 hãng xe ô tô niêm yết giá bán xe X là:
\(850 \cdot 0,{98^5} = 768,3326 \approx 768,333\) (triệu đồng).
Vậy 2025 hãng xe ô tô niêm yết giá bán xe X là \[768\,\,333\,\,000\] đồng. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận