Câu hỏi:

22/08/2024 217

Thống kê về số vật nuôi trong 98 hộ gia đình ta có kết quả sau:

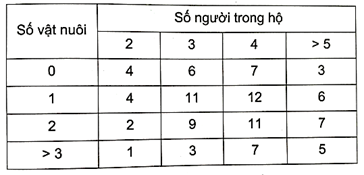
Chọn ngẫu nhiên một hộ gia đình. Tính xác suất để:

a) Hộ đó nuôi 2 vật nuôi biết rằng hộ đó có 4 người;

b) Hộ đó có 3 người biết rằng hộ đó có ít nhất 2 vật nuôi;

c) Hộ đó có ít nhất một vật nuôi, biết rằng hộ đó có ít nhất 4 người.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 12 Tập 2 KNTT Bài tập cuối chương VI có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Gọi A là biến cố: “Hộ đó nuôi 2 vật nuôi”.

B là biến cố: “Hộ đó có 4 người”.

Do đó, P(A | B) là xác suất hộ đó nuôi hai con, biết rằng hộ đó có 4 người.

Ta có: n(B) = 7 + 12 + 11 + 7 = 37, n(AB) = 11.

Do đó, P(B) = \(\frac{{37}}{{98}}\); P(AB) = \(\frac{{11}}{{98}}\).

Vậy P(A | B) = \(\frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{11}}{{37}}\).

b) Gọi C là biến cố: “Hộ đó có 3 người”;

D là biến cố: “Hộ đó có ít nhất 2 vật nuôi”.

Do đó, P(C | D) là xác suất hộ đó có 3 người biết rằng hộ đó có ít nhất 2 vật nuôi.

Ta có: n(D) = 29 + 16 = 45; n(CD) = 9 + 3 =12.

Do đó, P(D) = \(\frac{{45}}{{98}}\); P(CD) = \(\frac{{12}}{{98}}\).

Vậy P(C | D) = \(\frac{{P\left( {CD} \right)}}{{P\left( D \right)}} = \frac{{12}}{{45}} = \frac{4}{{15}}\).

c) Gọi E là biến cố: “Hộ đó có ít nhất một vật nuôi”;

F là biến cố: “Hộ đó có ít nhất 4 người”.

Do đó, P(E | F) là xác suất hộ đó có ít nhất một vật nuôi, biết rằng hộ đó có ít nhất 4 người.

Ta có: n(F) = 37 + 21 = 58, n(EF) = 30 + 18 = 48.

Do đó, P(F) = \(\frac{{58}}{{98}}\); P(EF) = \(\frac{{48}}{{98}}\).

Như vậy, P(E | F) = \(\frac{{P\left( {EF} \right)}}{{P\left( F \right)}} = \frac{{48}}{{58}} = \frac{{24}}{{29}}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chọn ngẫu nhiên một gia đình có 2 con. Biết rằng gia đình đó có con gái. Xác suất để gia đình đó có một con trai, một con gái là

A. \(\frac{2}{5}\).

B. \(\frac{3}{5}\).

C. \(\frac{3}{4}\).

D. \(\frac{2}{3}\).

Xem đáp án

Lời giải

Đáp án đúng là: D

Kí hiệu G là con gái, T là con trai.

Gọi E là biến cố: “Gia đình đó có một con trai, một con gái”.

F là biến cố: “Gia đình đó có con gái”.

Do đó, P(E | F) là xác suất chọn được gia đình có hai con gồm một trai, một gái.

Ta có: F = {GT; GG; TG}, n(F) = 3;

E = {GT; TG};

EF = {GT; TG}, n(EF) = 2.

Nên P(F) = \(\frac{3}{4}\), P(EF) = \(\frac{2}{4}\).

Suy ra P(E | F) = \(\frac{{P\left( {EF} \right)}}{{P\left( F \right)}} = \frac{2}{3}\).

Câu 2

Một lớp 12 có 40 học sinh. Trong đó có 22 em đăng kí thi Đại học quốc gia (ĐHQG), 25 em đăng kí thi Đại học bách khoa (ĐHBK), 3 em không đăng kí thi cả hai đại học này. Chọn ngẫu nhiên một học sinh. Biết rằng em đó đăng kí thi ĐHQG. Xác suất em đó đăng kí thi ĐHBK là

A. \(\frac{6}{{11}}\).

B. \(\frac{7}{{12}}\).

C. \(\frac{8}{{13}}\).

D. \(\frac{5}{{11}}\).

Xem đáp án

Lời giải

Đáp án đúng là: D

Gọi A là biến cố: “Em đó đăng kí thi ĐHQG”;

B là biến cố: “Em đó đăng kí thi ĐHBK”.

Ta có biến cố A ∪ B: “Em đó đăng kí thi ĐHQG hoặc ĐHBK” là biến cố dối của biến cố: “Em đó không đăng kí thi cả hai đại học này”.

P(A) = \(\frac{{22}}{{40}}\); P(B) = \(\frac{{25}}{{40}}\); P(\(\overline A \overline B \)) = \(\frac{3}{{40}}\).

Từ đó: P(A ∪ B) = 1 – P(\(\overline A \overline B \)) = 1 − \(\frac{3}{{40}}\) = \(\frac{{37}}{{40}}\).

P(AB) = P(A) + P(B) – P(A ∪ B) = \(\frac{{22}}{{40}} + \frac{{25}}{{40}} - \frac{{37}}{{40}} = \frac{{10}}{{40}}\).

Vậy P(B | A) = \(\frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{10}}{{40}}:\frac{{22}}{{40}} = \frac{{10}}{{22}} = \frac{5}{{11}}\).

Câu 3