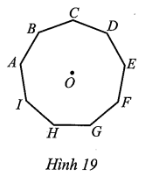
Cho hình đa giác đều có 9 cạnh ABCDEFGHI với tâm O (Hình 19). Tìm phát biểu sai, phát biểu đúng trong các phát biểu sau:
a) Các phép quay thuận chiều α° tâm O, với α° lần lượt nhận các giá trị 40°; 80°; …; 320°; 360° giữ nguyên hình đa giác đều ABCDEFGHI .
b) Phép quay ngược chiều 80° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm H, I, E, B, C.
c) Phép quay ngược chiều 120° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm G, H, I, A, C.
Cho hình đa giác đều có 9 cạnh ABCDEFGHI với tâm O (Hình 19). Tìm phát biểu sai, phát biểu đúng trong các phát biểu sau:
a) Các phép quay thuận chiều α° tâm O, với α° lần lượt nhận các giá trị 40°; 80°; …; 320°; 360° giữ nguyên hình đa giác đều ABCDEFGHI .
b) Phép quay ngược chiều 80° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm H, I, E, B, C.
c) Phép quay ngược chiều 120° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm G, H, I, A, C.
Câu hỏi trong đề: Giải SBT Toán 9 Bài 2. Phép quay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
– Phát biểu a) đúng.
– Vì phép quay ngược chiều 80° tâm O biến điểm C thành điểm A nên phát biểu phép quay ngược chiều 80° tâm O biến điểm C thành điểm E là sai. Vậy phát biểu b) sai.
– Vì phép quay ngược chiều 120° tâm O biến điểm E thành điểm B nên phát biểu phép quay ngược chiều 120° tâm O biến điểm E thành điểm C là sai. Vậy phát biểu c) sai.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
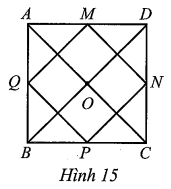
a) Xét ∆ABC có Q, P lần lượt là trung điểm của AB, BC nên QP là đường trung bình của tam giác, do đó QP // AC và \(QP = \frac{1}{2}AC.\)
Tương tự, ta có: MN là đường trung bình của tam giác ACD, do đó MN // AC và \(MN = \frac{1}{2}AC.\)
Do đó MNPQ là hình bình hành.
Mặt khác, ta cũng chứng minh được MQ là đường trung bình của ∆ABD nên \(MQ = \frac{1}{2}BD.\)
Lại có ABCD là hình vuông nên AC = BD và AC ⊥ BD.
Suy ra MN = MQ và MN ⊥ MQ.
Khi đó hình bình hành MNPQ là hình vuông.
b) ⦁ Phép quay ngược chiều 90° tâm O biến điểm O tương ứng thành chính nó.
⦁ Do ABCD là hình vuông tâm O nên OA = OB = OC = OD.
Theo câu a, ta có \(\widehat {AOD} = 90^\circ \)
Do đó, tia OD quay ngược chiều 90° tâm O đến tia OA.
⦁ Tương tự, đối với hình vuông MNPQ ta cũng có ON = OM và \(\widehat {NOM} = 90^\circ \) nên tia ON quay ngược chiều 90° tâm O đến tia OM.
Vậy phép quay ngược chiều 90° tâm O biến các điểm O, D, N tương ứng thành các điểm O, A, M.
c) Các phép quay tâm O giữ nguyên hình vuông MNPQ là các phép quay thuận chiều α° tâm O và các phép quay ngược chiều α° tâm O, với α° lần lượt nhận các giá trị:
α1° = 90°; α2° = 180°; α3° = 270°; α4° = 360°.
Lời giải
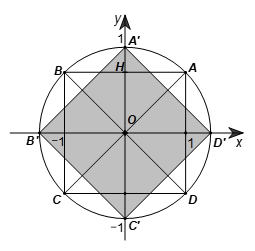
Gọi H là hình chiếu của A trên Oy.
Ta có A(1; 1) nên suy ra AH = OH = 1.
Do đó ∆OAH vuông cân tại H nên \(\widehat {AOH} = 45^\circ .\)
Xét ∆OAH vuông tại H, ta có: OA2 = OH2 + AH2 (định lí Pythagore)
Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 .\)
Tương tự, ta sẽ có \(OA = OB = OC = OD = \sqrt 2 .\)
Mặt khác, do ABCD là hình vuông nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường, do đó O là tâm của hình vuông.
Do đó, phép quay ngược chiều 45° tâm O biến điểm A thành các điểm A’ nằm trên tia Oy sao cho \(OA' = OA = \sqrt 2 ,\) tức là \[A'\left( {0;\sqrt 2 } \right).\]
Tương tự, ta chứng minh được, phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm \[A'\left( {0;\sqrt 2 } \right),\,\,B'\left( { - \sqrt 2 ;0} \right),\] \(C'\left( {0; - \sqrt 2 } \right),\,\,D'\left( {\sqrt 2 ;0} \right).\)
Suy ra tứ giác A’B’C’D’ là hình vuông với hai đường chéo là A’C’ và B’D’, nên diện tích tứ giác A’B’C’D’ là:
\(\frac{1}{2} \cdot A'C' \cdot B'D' = \frac{1}{2} \cdot 2\sqrt 2 \cdot 2\sqrt 2 = 4\) (đơn vị diện tích).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập