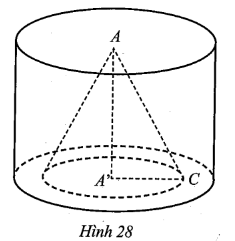
Từ một khối gỗ hình trụ (T) với hai đường tròn đáy là (A; R), (A’; R) và đường cao AA’ = h, người ta khoét đi một khối hình nón (N) có bán kính đường tròn đáy \(A'C = \frac{2}{3}R\) và đường cao trùng với đường cao của hình trụ (T) (Hình 28). Hỏi thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng bao nhiêu phần trăm thể tích của khối gỗ (T) ban đầu (làm tròn kết quả đến hàng phần mười)?
Từ một khối gỗ hình trụ (T) với hai đường tròn đáy là (A; R), (A’; R) và đường cao AA’ = h, người ta khoét đi một khối hình nón (N) có bán kính đường tròn đáy \(A'C = \frac{2}{3}R\) và đường cao trùng với đường cao của hình trụ (T) (Hình 28). Hỏi thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng bao nhiêu phần trăm thể tích của khối gỗ (T) ban đầu (làm tròn kết quả đến hàng phần mười)?
Câu hỏi trong đề: Giải SBT Toán 9 Bài tập cuối chương X đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thể tích của khối gỗ hình trụ (T) là: πR2h.
Thể tích của khối gỗ hình nón (N) là: \(\frac{1}{3}\pi \cdot {\left( {\frac{2}{3}R} \right)^2} \cdot h = \frac{4}{{27}}\pi {R^2}h.\)
Thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối gỗ hình nón (N) là
\(\pi {R^2}h - \frac{4}{{27}}\pi {R^2}h = \frac{{23}}{{27}}\pi {R^2}h.\)
Tỉ số phần trăm của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) so với thể tích của khối gỗ (T) ban đầu là \(\frac{{\frac{{23}}{{27}}\pi {R^2}h}}{{\pi {R^2}h}} \cdot 100\% \approx 85,2\% .\)
Vậy thể tích phần còn lại của khối gỗ (T) sau khi khoét bỏ khối hình nón (N) bằng khoảng 85,2% thể tích của khối gỗ (T) ban đầu.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có tổng thể tích của 4 viên bi thuỷ tinh hình cầu có cùng bán kính 3 cm là:
\(4 \cdot \left( {\frac{4}{3}\pi \cdot {3^3}} \right) = 144\pi \) (cm3).
Khi thả vào cốc nước 4 viên bi thuỷ tinh đó thì lượng nước trong cốc cao thêm độ cao h là: \(h = \frac{{144\pi }}{{\pi \cdot {4^2}}} = 9\) (cm).
Vậy sau khi thả vào cốc nước 4 viên bi thuỷ tinh đó, mực nước trong cốc cách miệng cốc một khoảng là: 20 – 9 – 9 = 2 (cm).
Lời giải
Gọi R (cm) và r (cm) lần lượt là bán kính đáy của hình trụ An và Bình đã cuộn (R > 0, r > 0).
Hình trụ An cuộn có chu vi đáy bằng 3a nên ta có 2πR = 3a, suy ra \(R = \frac{{3a}}{{2\pi }}\) (cm).
Hình trụ An cuộn có chu vi đáy bằng a nên ta có 2πr = a, suy ra \(r = \frac{a}{{2\pi }}\) (cm).
Thể tích của hình trụ bạn An cuộn là
\({V_1} = \pi {\left( {\frac{{3a}}{{2\pi }}} \right)^2} \cdot a = \frac{{9{a^3}}}{{4\pi }}\) (cm3).
Thể tích của hình trụ bạn Bình cuộn là
\({V_2} = \pi {\left( {\frac{a}{{2\pi }}} \right)^2} \cdot 3a = \frac{{3{a^3}}}{{4\pi }}\) (cm3).
Do đó, tỉ số của V1 và V2 là \[\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{{9{a^3}}}{{4\pi }}}}{{\frac{{3{a^3}}}{{4\pi }}}} = 3.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo