Câu hỏi:
28/08/2024 628
Người ta làm nóng chảy một quả cầu kim loại đặc có bán kính 4 cm để chế tạo một vật thể đặc dạng hình nón có bán kính đáy 4 cm. Tìm chiều cao của vật thể mới tạo thành.
Người ta làm nóng chảy một quả cầu kim loại đặc có bán kính 4 cm để chế tạo một vật thể đặc dạng hình nón có bán kính đáy 4 cm. Tìm chiều cao của vật thể mới tạo thành.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Thể tích của quả cầu là:
\(V = \frac{4}{3} \cdot \pi \cdot {4^3} = \frac{{256\pi }}{3}\) (cm3).
Thể tích của quả cầu là thể tích của vật thể hình nón được tạo thành.
Ta có thể tích của hình nón là: \(V = \frac{1}{3}\pi {r^2}h,\) suy ra:
\(h = \frac{{3V}}{{\pi {r^2}}} = \frac{{3 \cdot \frac{{256\pi }}{3}}}{{\pi \cdot {4^2}}} = 16\) (cm).
Vậy chiều cao của vật thể hình nón là 16 cm.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
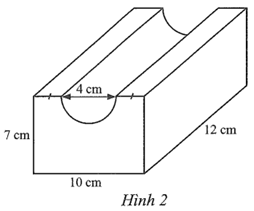
a) Thể tích của khối hộp chữ nhật khi chưa bị khoét là:
V1 = 12.10.7 = 840 (cm3).
Bán kính đáy của hình trụ là: 4 : 2 = 2 (cm).
Thể tích của nửa hình trụ là:
\({V_2} = \frac{1}{2} \cdot \left( {\pi \cdot {2^2} \cdot 12} \right) = 24\pi \) (cm3).
Thể tích của khối còn lại là:
V = V1 – V2 = 840 – 24π ≈ 765 (cm3).
b) Diện tích toàn phần của khối hộp khi chưa bị khoét là:
S1 = 2.7.(10 + 12) + 2.(10.12) = 548 (cm2).
Diện tích xung quanh của nửa hình trụ là:
\[{S_2} = \frac{1}{2} \cdot \left( {2\pi \cdot 2 \cdot 12} \right) = 24\pi \] (cm2).
Diện tích hai đáy của nửa hình trụ̣ là:
S3 = π.22 = 4π (cm2).
Diện tích mặt cắt dọc của nửa hình trụ là:
S4 = 4.12 = 48 (cm2).
Diện tích bề mặt của khối còn lại là:
S = S1 + S2 – S3 – S4 = 548 + 24π – 4π – 48 = 500 + 20π ≈ 563 (cm2).
Lời giải
Bán kính đáy của hình trụ là: 18 : 2 = 9 (cm).
Thể tích của nước ban đầu trong lọ là:
V1 = π.92.13,2 = 1 069,2 π (cm3).
Bán kính của quả cầu thép là: 12 : 2 = 6 (cm).
Thể tích của quả cầu thép là:
\({V_2} = \frac{4}{3} \cdot \pi \cdot {6^3} = 288\pi \) (cm3).
Thể tích của cột nước trong thùng sau khi thả quả cầu vào là:
V = V1 + V2 = 1 069,2π + 288π = 1 357,2π (cm3).
Chiều cao của mực nước sau khi thả quả cầu vào là:
\(h = \frac{{1357,2\pi }}{{\pi \cdot {9^2}}} \approx 16,76\) (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận