Giả sử ( int { frac{1}{{ sqrt[3]{{{{ rm{x}}^5}}}}}} { rm{dx}} = { rm{a}}{{ rm{x}}^{ frac{{ rm{m}}}{{ rm{n}}}}} + { rm{C}} ) với a là hằng số thực, n là số nguyên dương, m là số nguyên và ước số chung...

Đáp số: -0,5. ( int { frac{1}{{ sqrt[3]{{{x^5}}}}}} dx = int { frac{1}{{{x^{ frac{5}{3}}}}}} dx = int {{x^{ frac{{ - 5}}{3}}}} dx = frac{{{x^{ frac{{ - 5}}{3} + 1}}}}{{ frac{{ - 5}}{3} + 1}} + C = frac{{ - 3}}{2} frac{1}{{{x^{ frac{2}{3}}}}} + C = frac{{ - 3}}{2}{x^{ frac{{ - 2}}{3}}} + C ) (a + m + n = frac{{ - 3}}{2} - 2 + 3 = - 0,5 )

Giả sử ∫ 1 3 √ x 5 d x = a x m n + C với a là hằng số thực, n là số nguyên dương, m là số nguyên và ước số chung lớn nhất của m và n bằng 1. Giá trị của biểu thức S = a + m + n là bao nhi

Câu 1

Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với vận tốc ban đầu $29,4\;{\rm{m}}/{\rm{s}}.$ Quãng đường viên đạn đi được từ lúc bắn lên cho tới khi chạm đất là bao nhiêu mét? Biết gia tốc trọng trường là $9,8\;{\rm{m}}/{{\rm{s}}^2}.$

Xem đáp án

Lời giải

Đáp số: 88,2

${\rm{v}} = 29,4 - 9,8{\rm{t}},{\rm{v}} = 0 \Leftrightarrow 29,4 - 9,8{\rm{t}} = 0 \Leftrightarrow {\rm{t}} = 3$

$\;{\rm{S}} = 2\int_0^3 {(29,4 - 9,8{\rm{t}})} {\rm{dt}} = \left. {2\left( {29,4{\rm{t}} - 4,9{{\rm{t}}^2}} \right)} \right|_0^3 = 88,2(\;{\rm{m}})$

Câu 2

Một nhà thiết kế cần làm một cái logo có dạng hình chữ nhật kích thước $40\;{\rm{cm}} \times 80\;{\rm{cm}}.$ Trong logo đó có hai đường parabol chung đỉnh, cùng trục đối xứng chứa đường trung bình của hình chữ nhật và hai parabol đi qua đỉnh của hình chữ nhật (hình bên). Nhà thiết kế có kế hoạch làm màu nền là màu xanh phần phía trên của cả hai đường parabol và phần phía dưới của cả hai đường parabol, phần còn lại là màu khác. Diện tích phần màu xanh là bao nhiêu ${\rm{d}}{{\rm{m}}^2}$ (làm tròn kết quả đến hàng phần mười)?

$Một nhà thiết kế cần làm một cái logo có dạng hình chữ nhật kích thước $40\;{\rm{cm}} \times 80\;{\rm{cm}}.$ Trong logo đó có hai đường parabol chung đỉnh, cùng trục đối xứng chứa đường trung bình của hình chữ nhật và hai parabol đi qua đỉnh của hình chữ nhật (hình bên). Nhà thiết kế có kế hoạch làm màu nền là màu xanh phần phía trên của cả hai đường parabol và phần phía dưới của cả hai đường parabol, phần còn lại là màu khác. Diện tích phần màu xanh là bao nhiêu ${\rm{d}}{{\rm{m}}^2}$ (làm tròn kết quả đến hàng phần mười)? (ảnh 1)$

Xem đáp án

Lời giải

Đáp số: 10,7.

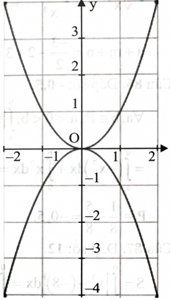
$Một nhà thiết kế cần làm một cái logo có dạng hình chữ nhật kích thước $40\;{\rm{cm}} \times 80\;{\rm{cm}}.$ Trong logo đó có hai đường parabol chung đỉnh, cùng trục đối xứng chứa đường trung bình của hình chữ nhật và hai parabol đi qua đỉnh của hình chữ nhật (hình bên). Nhà thiết kế có kế hoạch làm màu nền là màu xanh phần phía trên của cả hai đường parabol và phần phía dưới của cả hai đường parabol, phần còn lại là màu khác. Diện tích phần màu xanh là bao nhiêu ${\rm{d}}{{\rm{m}}^2}$ (làm tròn kết quả đến hàng phần mười)? (ảnh 2)$

Chọn hệ trục toạ độ Oxy như hình bên với đơn vị của hai trục là dm.

Đường parabol phía trên có phương trình ${\rm{y}} = {\rm{a}}{{\rm{x}}^2}$ và đi qua các điểm $( - 2;4),(2;4).$

Suy ra ${\rm{a}} = 1.$

Đường parabol phía dưới có phương trình ${\rm{y}} = {{\rm{a}}^\prime }{{\rm{x}}^2}$ và đi qua các điểm $( - 2; - 4),(2; - 4).$

Suy ra ${{\rm{a}}^\prime } = - 1.$ Diện tích của hình chữ nhật là $4.8 = 32\left( {{\rm{d}}{{\rm{m}}^2}} \right).$

Diện tích phần màu xanh bằng diện tích hình phẳng giới hạn bởi hai đường parabol ${\rm{y}} = {{\rm{x}}^2}$, $y = - {x^2}$ và các đường thẳng $x = - 2,x = 2.$

Ta có $S = \int_{ - 2}^2 {\left| {{x^2} - \left( { - {x^2}} \right)} \right|} dx = \left. {\frac{{2{x^3}}}{3}} \right|_{ - 2}^2 = \frac{{32}}{3} \approx 10,7\left( {{\rm{d}}{{\rm{m}}^2}} \right).$

Câu 3