Câu hỏi:
23/09/2024 290
Từ câu 37 đến câu 50: Cho hình lập phương \({\rm{ABCD}}.{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) cạnh a.
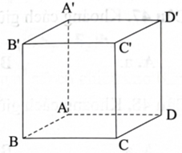Khoảng cách từ điểm A đến đường thẳng BC bằng
Từ câu 37 đến câu 50: Cho hình lập phương \({\rm{ABCD}}.{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\) cạnh a.
Đáp án chính xác
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
\({\rm{d}}({\rm{A}},{\rm{BC}}) = {\rm{AB}} = {\rm{a}}.\) Chọn A.
Câu hỏi cùng đoạn
Câu 2:
Khoảng cách từ điểm A đến đường thẳng BD bằng
Đáp án chính xác
Lời giải của GV VietJack
Gọi O là hình chiếu của A trên \(BD,d(A,BD) = AO\) \( = \frac{{{\rm{a}}\sqrt 2 }}{2}.\) Chọn D.
Câu 3:
Khoảng cách từ điểm A đến đường thẳng CC ' bằng
Đáp án chính xác
Lời giải của GV VietJack
Vì \(AC \bot C{C^\prime }\) nên \(d\left( {A,C{C^\prime }} \right) = AC = a\sqrt 2 .\) Chọn B.
Câu 4:
Khoảng cách từ điểm A đến mặt phẳng (\({{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\)) bằng
Đáp án chính xác
Lời giải của GV VietJack
Vì \(A{A^\prime } \bot \left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)\) nên \(d\left( {A,\left( {{A^\prime }{B^\prime }{C^\prime }{D^\prime }} \right)} \right) = A{A^\prime } = a.\) Chọn A.
Câu 5:
Khoảng cách từ điểm A đến mặt phẳng (BDD'B') bằng
Đáp án chính xác
Lời giải của GV VietJack
O là hình chiếu của A trên \({\rm{BD}},{\rm{d}}({\rm{A}},{\rm{BD}}) = {\rm{AO}} = \frac{{{\rm{a}}\sqrt 2 }}{2}.\)
Vì \(AO \bot \left( {{B^\prime }{D^\prime }{B^\prime }} \right)\) nên \(d\left( {A,\left( {BD{D^\prime }{B^\prime }} \right)} \right) = AO = \frac{{a\sqrt 2 }}{2}.\) Chọn D.
Câu 6:
Khoảng cách từ đường thẳng \({\rm{D}}{{\rm{D}}^\prime }\) đến mặt phẳng ( \({\rm{AB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }\) ) bằng
Đáp án chính xác
Lời giải của GV VietJack
d(DD', \(\left. {\left( {{\rm{AB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }} \right)} \right) = {\rm{DA}} = {\rm{a}}.\) Chọn A.
Câu 7:
Khoảng cách từ đường thẳng \({\rm{D}}{{\rm{D}}^\prime }\) đến mặt phẳng ( \({\rm{AC}}{{\rm{C}}^\prime }{{\rm{A}}^\prime }\) ) bằng
Đáp án chính xác
Lời giải của GV VietJack
\(O\) là hình chiếu của \(D\) trên AC.
Vì \(DO \bot \left( {AC{C^\prime }{A^\prime }} \right)\) nên \(d\left( {D,\left( {AC{C^\prime }{A^\prime }} \right)} \right) = DO = \frac{{a\sqrt 2 }}{2}.\) Chọn D.
Câu 8:
Khoảng cách giữa hai mặt phẳng (\({\rm{AD}}{{\rm{D}}^\prime }{{\rm{A}}^\prime }\)) và (\({\rm{BC}}{{\rm{C}}^\prime }{{\rm{B}}^\prime }\)) bằng
Đáp án chính xác
Lời giải của GV VietJack
d ((ADD'A'), (BCC'B')) = \({\rm{AB}} = {\rm{a}}.\) Chọn A.
Câu 9:
Khoảng cách giữa hai đường thẳng AB và CD bằng
Đáp án chính xác
Lời giải của GV VietJack
\(d(AB,CD) = AD = a.\) Chọn A.
Câu 10:
Khoảng cách giữa hai đường thẳng AB và C ' D ' bằng
Đáp án chính xác
Lời giải của GV VietJack
\({\rm{d}}\left( {{\rm{AB}},{{\rm{C}}^\prime }{{\rm{D}}^\prime }} \right) = {\rm{A}}{{\rm{D}}^\prime } = {\rm{a}}\sqrt 2 .\) Chọn B.
Câu 11:
Khoảng cách giữa hai đường thẳng AB và \({\rm{D}}{{\rm{D}}^\prime }\) bằng
Đáp án chính xác
Lời giải của GV VietJack
\({\rm{d}}\left( {AB,D{D^\prime }} \right) = AD = a.\) Chọn A.
Câu 12:
Khoảng cách giữa hai đường thẳng BD và \({\rm{A}}{{\rm{A}}^\prime }\) bằng
Đáp án chính xác
Lời giải của GV VietJack
\(O\) là hình chiếu của \(A\) trên \(BD \cdot d\left( {BD,{A^\prime }} \right) = AO = \frac{{a\sqrt 2 }}{2}.\) Chọn D.
Câu 13:
Khoảng cách giữa hai đường thẳng BD và \({{\rm{A}}^\prime }{{\rm{C}}^\prime }\) bằng
Đáp án chính xác
Lời giải của GV VietJack
Khoảng cách giữa hai đường thẳng chéo nhau $B D$ và \({A^\prime }{C^\prime }\) bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó \({\rm{d}}\left( {{\rm{BD}},{{\rm{A}}^\prime }{{\rm{C}}^\prime }} \right) = {\rm{d}}\left( {({\rm{ABCD}}),\left( {{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }} \right)} \right) = {\rm{A}}{{\rm{A}}^\prime } = {\rm{a}}.\) Chọn A.
Câu 14:
Gọi \(\Delta \) và \({\Delta ^\prime }\) là hai đường thẳng chéo nhau lần lượt thuộc hai mặt phẳng \(({\rm{ABCD}})\) và \(\left( {{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }} \right).\) Khoảng cách giữa hai đường thẳng \(\Delta \) và \({\Delta ^\prime }\) bằng
Đáp án chính xác
Lời giải của GV VietJack
Khoảng cách giữa hai đường thẳng chéo nhau \(\Delta \) và \({\Delta ^\prime }\) bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó \({\rm{d}}\left( {\Delta ,{\Delta ^\prime }} \right) = {\rm{d}}\left( {({\rm{ABCD}}),\left( {{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }} \right)} \right) = {\rm{A}}{{\rm{A}}^\prime } = {\rm{a}}.\) Chọn A.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Khoảng cách từ điểm A đến mặt phẳng (\({{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }\)) bằng
Xem đáp án »
23/09/2024
0
Câu 5:
Khoảng cách từ đường thẳng \({\rm{D}}{{\rm{D}}^\prime }\) đến mặt phẳng ( \({\rm{AB}}{{\rm{B}}^\prime }{{\rm{A}}^\prime }\) ) bằng
Xem đáp án »
23/09/2024
0
Câu 6:
Khoảng cách từ đường thẳng \({\rm{D}}{{\rm{D}}^\prime }\) đến mặt phẳng ( \({\rm{AC}}{{\rm{C}}^\prime }{{\rm{A}}^\prime }\) ) bằng
Xem đáp án »
23/09/2024
0
về câu hỏi!