Câu hỏi:

23/09/2024 618

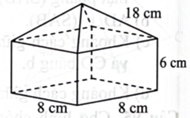
Hình bên là hình biểu diễn của vật thể ghép bởi khối hộp chữ nhật với ba kích thước 12 m, $25\;{\rm{m}},18\;{\rm{m}}$ và khối lăng trụ tam giác có một chiều cao của mặt đáy là 8 m. Vật thể đó có thể tích bằng bao nhiêu ${{\rm{m}}^3}$ ?

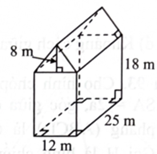
$Hình bên là hình biểu diễn của vật thể ghép bởi khối hộp chữ nhật với ba kích thước 12 m, \và khối lăng trụ tam giác có một chiều cao của mặt đáy là 8 m. \ (ảnh 1)$

Câu hỏi trong đề: Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 6: Hình học và đo lường trong không gian có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp số: 6600.

Khối đã cho được tạo thành từ khối lăng trụ và khối hộp chữ nhật.

Thể tích khối lăng trụ là: $\frac{1}{2} \cdot 8 \cdot 12 \cdot 25 = 1200\left( {\;{{\rm{m}}^3}} \right).$

Thể tích khối hộp chữ nhật là: $18 \cdot 25 \cdot 12 = 5400\left( {\;{{\rm{m}}^3}} \right).$

Thể tích của khối đã cho là: $6600\;{{\rm{m}}^3}.$

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình lập phương ${\rm{ABCD}}.{{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }.$ Góc nhị diện $\left[ {{\rm{A}},{\rm{BB}}} \right.$ ', $\left. {{{\rm{D}}^\prime }} \right]$ có số đo bằng ${{\rm{n}}^o}$ với n là số dương. Giá trị của n bằng bao nhiêu?

Xem đáp án

Lời giải

Đáp số: 45.

Vì ${{\rm{B}}^\prime }{\rm{B}} \bot ({\rm{ABCD}})$ nên góc nhị diện $\left[ {{\rm{A}},{\rm{BB}},{{\rm{D}}^\prime }} \right]$ có số đo bằng $\widehat {{\rm{ABD}}}.$

Câu 2

Cho hình chóp S.ABCD có $SA = a\sqrt 3 ,SA \bot (ABCD),ABCD$ là hình vuông cạnh a. Gọi E là điểm thoả mãn $\overrightarrow {{\rm{AE}}} = - \frac{1}{2}\overrightarrow {{\rm{AB}}} .$ Khoảng cách từ điểm B đến mặt phẳng $({\rm{SDE}})$ bằng ${\rm{x}}\sqrt 3 {\rm{a}}$ với x là số thực. Giá trị của x là bao nhiêu?

Xem đáp án

Lời giải

Đáp số: 0,75.

$Cho hình chóp S.ABCD có $SA = a\sqrt 3 ,SA \bot (ABCD),ABCD$ là hình vuông cạnh a. Gọi E là điểm thoả mãn $\overrightarrow {{\rm{AE}}} = - \frac{1}{2}\overrightarrow {{\rm{AB}}} .$ Khoảng cách từ điểm B đến mặt phẳng $({\rm{SDE}})$ bằng ${\rm{x}}\sqrt 3 {\rm{a}}$ với x là số thực. Giá trị của x là bao nhiêu? (ảnh 1)$

+) $\frac{{{\rm{d}}({\rm{B}},({\rm{SDE}}))}}{{{\rm{d}}({\rm{A}},({\rm{SDE}}))}} = \frac{{{\rm{BE}}}}{{{\rm{AE}}}} = 3 \Rightarrow {\rm{d}}({\rm{B}},({\rm{SDE}})) = 3\;{\rm{d}}(\;{\rm{A}},({\rm{SDE}})).$(1)

+) Kẻ ${\rm{AM}} \bot {\rm{DE}}({\rm{M}} \in {\rm{DE}});{\rm{AH}} \bot {\rm{SM}}({\rm{H}} \in {\rm{SM}})$

$ \Rightarrow {\rm{AH}} \bot ({\rm{SDE}}) \Rightarrow {\rm{d}}({\rm{A}},({\rm{SDE}})) = {\rm{AH}}.$(2)

+) Ta có: $\frac{1}{{{\rm{A}}{{\rm{H}}^2}}} = \frac{1}{{{\rm{A}}{{\rm{S}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{M}}^2}}} = \frac{1}{{{\rm{A}}{{\rm{S}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{D}}^2}}} + \frac{1}{{{\rm{A}}{{\rm{E}}^2}}}$$ = \frac{1}{{{{(a\sqrt 3 )}^2}}} + \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} = \frac{{16}}{{3{a^2}}}$

$ \Rightarrow {\rm{AH}} = \frac{{{\rm{a}}\sqrt 3 }}{4}$(3)

Từ $(1),(2),(3) \Rightarrow d(B,(SDE)) = \frac{{3\sqrt 3 a}}{4} = 0,75 \cdot \sqrt 3 a.$

Câu 3

Bạn Thuý cần gấp một hộp có dạng hình hộp đứng với chiều cao là 40 cm và diện tích xung quanh là $2400\;{\rm{c}}{{\rm{m}}^2}.$ Khối hộp mà bạn Thuý cần gấp có thể tích lớn nhất bằng bao nhiêu ${\rm{c}}{{\rm{m}}^3}$ ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Hình bên là hình biểu diễn của khối vật thể có bốn mặt tam giác cân bằng nhau, bốn mặt hình chữ nhật và đáy là hình vuông. Thể tích của khối vật thể đó là bao nhiêu ${\rm{c}}{{\rm{m}}^3}$ (làm tròn kết quả đến hàng đơn vị)?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình lập phương ${\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }.$ Góc giữa đường thẳng AB ' và mặt phẳng $({\rm{ABCD}})$ bằng ${{\rm{n}}^^\circ }$ với n là số dương. Giá trị của n bằng bao nhiêu?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hình bên là hình biểu diễn của khối chóp tứ giác đều có độ dài cạnh đáy bằng 7 cm và độ dài trung đoạn bằng 9 cm. Khối chóp đó có thể tích bằng bao nhiêu ${\rm{c}}{{\rm{m}}^3}$ (làm tròn kết quả đến hàng đơn vị )?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bạn Thuý cần gấp một hộp có dạng hình hộp đứng với chiều cao là 40 cm và diện tích xung quanh là \(2400\;{\rm{c}}{{\rm{m}}^2}.\) Khối hộp mà bạn Thuý cần gấp có thể tích lớn nhất bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) ?

Hình bên là hình biểu diễn của khối vật thể có bốn mặt tam giác cân bằng nhau, bốn mặt hình chữ nhật và đáy là hình vuông. Thể tích của khối vật thể đó là bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) (làm tròn kết quả đến hàng đơn vị)?

Cho hình lập phương \({\rm{ABCD}} \cdot {{\rm{A}}^\prime }{{\rm{B}}^\prime }{{\rm{C}}^\prime }{{\rm{D}}^\prime }.\) Góc giữa đường thẳng AB ' và mặt phẳng \(({\rm{ABCD}})\) bằng \({{\rm{n}}^^\circ }\) với n là số dương. Giá trị của n bằng bao nhiêu?

Hình bên là hình biểu diễn của khối chóp tứ giác đều có độ dài cạnh đáy bằng 7 cm và độ dài trung đoạn bằng 9 cm. Khối chóp đó có thể tích bằng bao nhiêu \({\rm{c}}{{\rm{m}}^3}\) (làm tròn kết quả đến hàng đơn vị )?