Cho \(a < b.\) Khi đó

a) \(4a - 2 > 4b - 2.\)                                           b) \(6 - 3a < 6 - 3b\).

c) \(4a + 1 < 4b + 5.\)                                         d) \(7 - 2a > 4 - 2b.\)

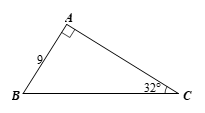
a) Xét \(\Delta ABC\) vuông tại \(A,\) ta có:

⦁ \(\sin C = \frac{{AB}}{{BC}},\) suy ra \(BC = \frac{{AB}}{{\sin C}} = \frac{9}{{\sin 32^\circ }} \approx 16,98.\)

⦁ \(AC = AB \cdot \cot C = 9 \cdot \cot 32^\circ  \approx 14,40.\)

Vậy \[AC \approx 14,40\] và \[BC \approx 16,98.\]

b) Xét \(\Delta ABC\) vuông tại \(A,\) ta có:

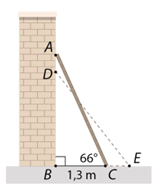
\(BC = AC \cdot \cos C\), suy ra \(AC = \frac{{BC}}{{\cos C}} = \frac{{1,3}}{{\cos 66^\circ }} \approx 3,20\) (m).

Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(AB = BC \cdot \tan C = 1,3 \cdot \tan 66^\circ  \approx 2,92\) (m).

Khi đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}} = 0,4{\rm{\;m}}\) đến vị trí \(D\) thì \(DB = AB - AD \approx 2,92 - 0,4 = 2,52\) (m) và chiều dài thang là \(DE = AC \approx 3,20\) (m).

Xét \(\Delta BDE\) vuông tại \(B,\) ta có:

\(\sin \widehat {DEB} = \frac{{BD}}{{DE}} \approx \frac{{2,52}}{{3,2}} = 0,7875\), suy ra \(\widehat {DEB} \approx 51^\circ 57'.\)

a) Vì số nguyên tử của \({\rm{K,}}\,\,{\rm{N}}\) và \({\rm{O}}\) ở cả hai vế của phương trình phản ứng phải bằng nhau nên ta có hệ phương trình: \(\left\{ \begin{array}{l}x = 2\\x = 2\\3x = 2 \cdot 2 + 2y\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = 2\\3x = 4 + 2y.\end{array} \right.\)

Thay \(x = 2\) vào phương trình \(3x = 4 + 2y,\) ta được:

\(3 \cdot 2 = 4 + 2y,\) suy ra \(2y = 2\) nên \(y = 1.\)

Vậy \(x = 2\) và \(y = 1.\) Khi đó ta có phương trình phản ứng hóa học sau khi được cân bằng như sau:

\(2{\rm{KN}}{{\rm{O}}_3} \to 2{\rm{KN}}{{\rm{O}}_2} + {{\rm{O}}_2}.\)

b) Gọi \(x,\,\,y\) (sản phẩm) lần lượt là số sản phẩm của tổ I và tổ II theo kế hoạch cần sản xuất \(\left( {x > 0,\,\,y > 0} \right)\).

Theo bài, theo kế hoạch hai tổ sản xuất 600 sản phẩm nên ta có phương trình: \(x + y = 600\) (1)

Khi tổ I vượt kế hoạch 18% thì số sản phẩm tổ I sản xuất được là: \(x + 18\% x = 1,18x\) (sản phẩm).

Khi tổ II vượt kế hoạch 21% thì số sản phẩm tổ II sản xuất được là: \(y + 21\% y = 1,21y\) (sản phẩm).

Theo bài, cả hai tổ đã hoàn thành vượt mức 120 sản phẩm nên ta có phương trình:

\(1,18x + 1,21y = 600 + 120\) hay \(118x + 121y = 72\,\,000\)   (2)

Từ phương trình (1) và phương trình (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 600\\118x + 121y = 72\,\,000\end{array} \right.\)

Nhân hai vế của phương trình thứ nhất của hệ trên với 118, ta được: \(\left\{ \begin{array}{l}118x + 118y = 70\,\,800\\118x + 121y = 72\,\,000\end{array} \right.\)

Trừ hai vế của phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:

\( - 3y =  - 1\,\,200\), suy ra \(y = 400\) (thỏa mãn).

Thay \(y = 400\) vào phương trình \(x + y = 600\), ta được:

\(x + 400 = 600\), suy ra \(x = 200\) (thỏa mãn).

Vậy theo kế hoạch, tổ I và tổ II cần sản xuất lần lượt là 200 sản phẩm và 400 sản phẩm.