Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có: \(y' = 3\left( {x - 3} \right) \cdot {e^x} + {\left( {x - 3} \right)^2} \cdot {e^x} = {e^x} \cdot \left( {x - 3} \right) \cdot \left( {x - 1} \right)\).
Khi đó, trên khoảng \(\left( {2;\,\,4} \right)\), \(y' = 0\) khi \(x = 3\).
\(y\left( 2 \right) = {e^2};\,\,y\left( 3 \right) = 0;\,\,y\left( 4 \right) = {e^4}\).
Từ đó suy ra \(\mathop {\max }\limits_{\left[ {2;\,4} \right]} y = y\left( 4 \right) = {e^4}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đ, b) S, c) S, d) Đ.
Hướng dẫn giải
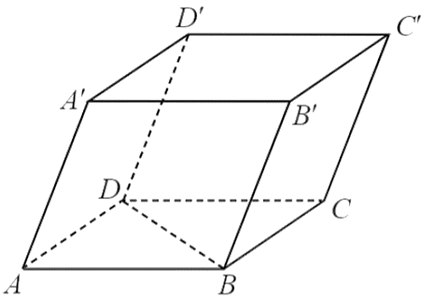
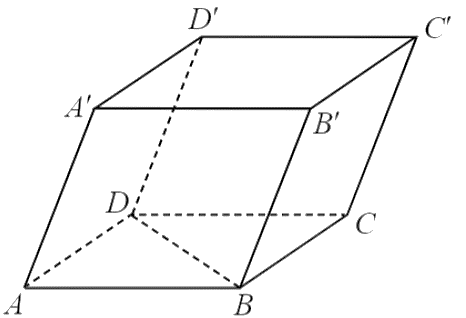
– Vì \(ABCD.A'B'C'D'\) là hình hộp nên các mặt của hình hộp này là hình bình hành.
Do đó, \(\overrightarrow {AD} = \overrightarrow {BC} = \overrightarrow {B'C'} = \overrightarrow {A'D'} \). Vậy ý a) đúng.
– Ta có \(\overrightarrow {DB} = - \overrightarrow {BD} \) và \(\overrightarrow {DB} = \overrightarrow {D'B'} = - \overrightarrow {B'D'} \).
Vậy các vectơ đối của vectơ \(\overrightarrow {DB} \) là \[\overrightarrow {BD} ,\,\,\overrightarrow {B'D'} \]. Do đó ý b) sai.
– Vì \(\overrightarrow {AB} = \overrightarrow {DC} = \overrightarrow {D'C'} \) nên \(\overrightarrow {AB} + \overrightarrow {DC} = \overrightarrow {D'C'} + \overrightarrow {D'C'} = 2\overrightarrow {D'C'} \).
Vậy ý c) sai.
– Ta có \(\overrightarrow {BB'} = \overrightarrow {AA'} ,\,\,\overrightarrow {CA} = \overrightarrow {C'A'} \). Suy ra \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {AA'} - \overrightarrow {C'A'} = \overrightarrow {AA'} + \overrightarrow {A'C'} = \overrightarrow {AC'} \).
Vậy ý d) đúng.
Lời giải
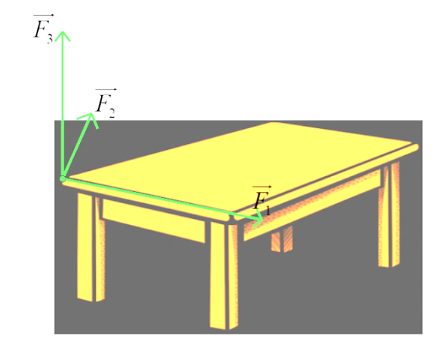
Theo đề bài, ta có hình vẽ sau:
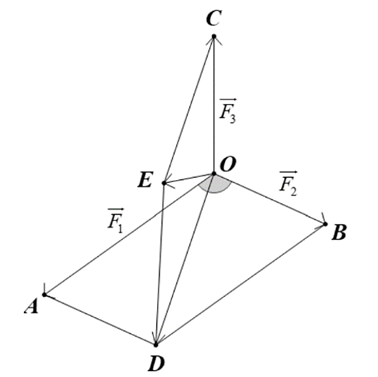
Hợp lực tác động vào ba vật là \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \).
Ta có \(\widehat {AOB} = \left( {\overrightarrow {OA} ,\,\overrightarrow {OB} } \right) = \left( {\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} } \right) = 110^\circ \). Suy ra \(\widehat {OAD} = 70^\circ \).
Áp dụng định lý côsin trong tam giác \(OAD\), ta có:
\(O{D^2} = O{A^2} + A{D^2} - 2OA \cdot AD \cdot \cos \widehat {OAD} = {9^2} + {4^2} - 2 \cdot 9 \cdot 4 \cdot \cos 70^\circ = 97 - 72\cos 70^\circ \).
Vì \(OC \bot \left( {OBDA} \right)\) nên \(OC \bot OD\). Suy ra \(ODEC\) là hình chữ nhật.
Do đó, tam giác \(OCE\) vuông tại \(C\) nên
\(O{E^2} = O{C^2} + E{C^2} = {7^2} + 97 - 72\cos 70^\circ = 146 - 72\cos 70^\circ \).
Suy ra \(OE = \sqrt {146 - 72\cos 70^\circ } \approx 11\).
Vậy độ lớn của hợp lực của ba lực đã cho bằng khoảng 11 N.
Đáp số: \(11\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.