Cho hai đồ thị G3 (Hình 3) và G4 (Hình 4). Dùng thuật toán duyệt đồ thị theo chiều rộng để
thực hiện hai yêu cầu sau:
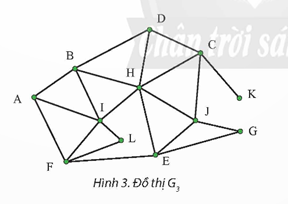
- Liệt kê thứ tự duyệt các đỉnh của đồ thị G3 xuất phát từ đỉnh A.
- Cho biết đường đi từ đỉnh F đến đỉnh J trong đồ thị G4 ?
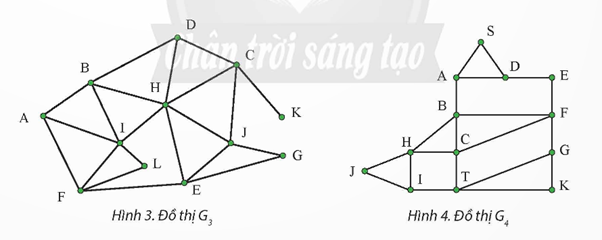
Cho hai đồ thị G3 (Hình 3) và G4 (Hình 4). Dùng thuật toán duyệt đồ thị theo chiều rộng để
thực hiện hai yêu cầu sau:
- Liệt kê thứ tự duyệt các đỉnh của đồ thị G3 xuất phát từ đỉnh A.
- Cho biết đường đi từ đỉnh F đến đỉnh J trong đồ thị G4 ?
Câu hỏi trong đề: Chuyên đề Tin 12 CTST Bài 3.3. Duyệt đồ thị theo chiều rộng !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Để thực hiện thuật toán duyệt đồ thị theo chiều rộng (BFS) cho đồ thị G3 và G4:
Đồ thị G3 xuất phát từ đỉnh A:
Bắt đầu từ đỉnh A.
Thăm các đỉnh kề với A theo thứ tự từ trái sang phải hoặc từ trên xuống dưới.
Tiếp tục quá trình này cho đến khi tất cả các đỉnh đều được thăm.
Đường đi từ đỉnh F đến đỉnh J trong đồ thị G4:
Xác định một chuỗi các cạnh liên kết từ F đến J.
Duyệt theo chiều rộng từ F, thăm các đỉnh kề và tiếp tục cho đến khi đến được J.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
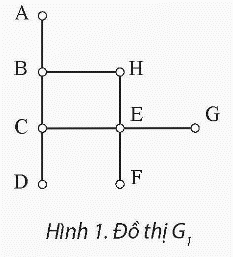
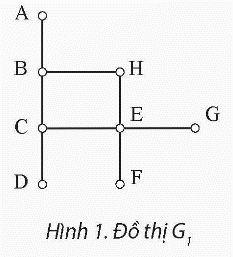
a. Để tìm đường đi ngắn nhất từ đỉnh C đến tất cả các đỉnh khác trong đồ thị G1 bằng thuật toán duyệt theo chiều rộng (BFS), ta thực hiện các bước sau:
Bắt đầu từ đỉnh C.
Thăm tất cả các đỉnh kề với C trước khi chuyển sang các đỉnh ở cấp độ tiếp theo.
Tiếp tục quá trình này cho đến khi tất cả các đỉnh đều được thăm.
b. Cách duyệt cây theo chiều rộng từ đỉnh C:
Bắt đầu từ đỉnh C, thăm các đỉnh kề theo thứ tự từ trái sang phải hoặc từ trên xuống dưới.
Đảm bảo rằng mỗi cấp độ của cây được duyệt hoàn toàn trước khi chuyển sang cấp độ tiếp theo.
Ghi nhớ các đỉnh đã thăm để tránh thăm lại.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
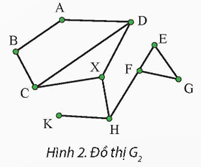
Dựa vào mô tả của “Hình 2. Đồ thị G,” để thực hiện duyệt đồ thị theo chiều rộng (BFS) bắt đầu từ đỉnh X, ta sẽ thăm tất cả các đỉnh kề với X trước khi chuyển sang các đỉnh khác. Một thứ tự duyệt có thể là:
Bắt đầu từ X
Duyệt đến A, B, C, D, E, F, H, K, G
Lưu ý rằng có thể có nhiều thứ tự duyệt đúng do cách chọn đỉnh kề khi duyệt có thể khác nhau. Thứ tự trên giả định rằng khi có nhiều đỉnh kề chưa được thăm, chúng ta sẽ thăm theo thứ tự bảng chữ cái.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập