Chuyên đề Tin 12 CTST Bài 3.3. Duyệt đồ thị theo chiều rộng

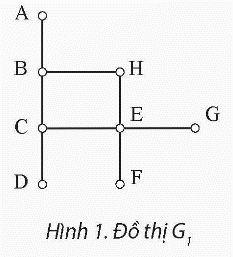
Dựa vào mô tả của đồ thị trong Hình 1, có một hành trình từ địa điểm D đến địa điểm G với ít địa điểm trung gian nhất. Hành trình ngắn nhất là:

Hành trình từ D đến G:

Đi từ D -> E

Tiếp tục từ E -> G

Đây là hành trình tối ưu nhất với chỉ một địa điểm trung gian là E. Đường đi này giúp rút ngắn thời gian và quãng đường di chuyển giữa hai địa điểm D và G.

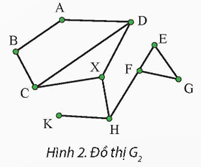
Dựa vào mô tả của “Hình 2. Đồ thị G,” để thực hiện duyệt đồ thị theo chiều rộng (BFS) bắt đầu từ đỉnh X, ta sẽ thăm tất cả các đỉnh kề với X trước khi chuyển sang các đỉnh khác. Một thứ tự duyệt có thể là:

Bắt đầu từ X

Duyệt đến A, B, C, D, E, F, H, K, G

Lưu ý rằng có thể có nhiều thứ tự duyệt đúng do cách chọn đỉnh kề khi duyệt có thể khác nhau. Thứ tự trên giả định rằng khi có nhiều đỉnh kề chưa được thăm, chúng ta sẽ thăm theo thứ tự bảng chữ cái.

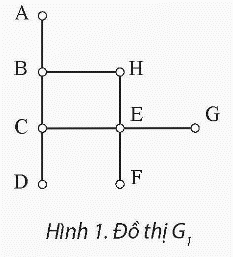
a. Để tìm đường đi ngắn nhất từ đỉnh C đến tất cả các đỉnh khác trong đồ thị G1 bằng thuật toán duyệt theo chiều rộng (BFS), ta thực hiện các bước sau:

Bắt đầu từ đỉnh C.

Thăm tất cả các đỉnh kề với C trước khi chuyển sang các đỉnh ở cấp độ tiếp theo.

Tiếp tục quá trình này cho đến khi tất cả các đỉnh đều được thăm.

b. Cách duyệt cây theo chiều rộng từ đỉnh C:

Bắt đầu từ đỉnh C, thăm các đỉnh kề theo thứ tự từ trái sang phải hoặc từ trên xuống dưới.

Đảm bảo rằng mỗi cấp độ của cây được duyệt hoàn toàn trước khi chuyển sang cấp độ tiếp theo.

Ghi nhớ các đỉnh đã thăm để tránh thăm lại.

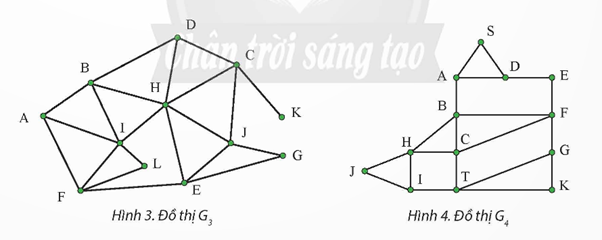
Để thực hiện thuật toán duyệt đồ thị theo chiều rộng (BFS) cho đồ thị G3 và G4:

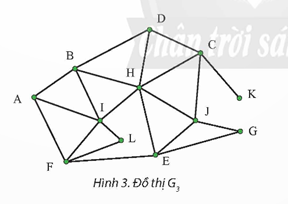
Đồ thị G3 xuất phát từ đỉnh A:

Bắt đầu từ đỉnh A.

Thăm các đỉnh kề với A theo thứ tự từ trái sang phải hoặc từ trên xuống dưới.

Tiếp tục quá trình này cho đến khi tất cả các đỉnh đều được thăm.

Đường đi từ đỉnh F đến đỉnh J trong đồ thị G4:

Xác định một chuỗi các cạnh liên kết từ F đến J.

Duyệt theo chiều rộng từ F, thăm các đỉnh kề và tiếp tục cho đến khi đến được J.

Dựa vào mô tả hình ảnh của đồ thị G3, để duyệt đồ thị bắt đầu từ đỉnh B và đỉnh F, chúng ta sẽ sử dụng thuật toán duyệt theo chiều rộng (BFS). Thứ tự duyệt sẽ phụ thuộc vào cách các đỉnh được kết nối trong đồ thị. Khi bắt đầu từ đỉnh B, chúng ta sẽ thăm các đỉnh kề với B trước, sau đó là các đỉnh kề với những đỉnh đã thăm, và cứ tiếp tục như vậy. Tương tự, khi bắt đầu từ đỉnh F, chúng ta sẽ thăm các đỉnh kề với F theo cùng một cách thức.

Để có nhận xét chính xác về thứ tự duyệt, em cần thông tin cụ thể về cách các đỉnh được kết nối cũng như các quy tắc duyệt nếu có. Nếu bạn cung cấp thêm thông tin hoặc mã nguồn của chương trình, em có thể giúp bạn phân tích cụ thể hơn.

Code như sau:

def bft(graph, u): queue initQueue()

visited [vertices.index(u)] = True enqueue(queue, u)

while not is EmptyQueue (queue): u = dequeue(queue) print(u, end = "") for v in graph[u]:

if not visited[vertices.index(v)]:

visited[vertices.index(v)] = True enqueue(queue, v)

#Khởi tạo queue rỗng #Đánh dấu đỉnh u đã duyệt #Thêm đỉnh u vào queue #queue khác rỗng

#Lấy đỉnh u ra khỏi queue #Xử lí đỉnh u

#Xét đỉnh kề v của đỉnh u #Đỉnh v chưa duyệt

#Đánh dấu đỉnh v đã duyệt #Thêm đỉnh v vào queue

#Hàm duyệt graph dạng danh sách kề theo chiều rộng

def bfs(graph):

global visited

visited

[False] * len(graph)

for u in graph:

if not visited [vertices.index(u)]:

bft (graph, u)

#Đánh dấu các đỉnh chưa duyệt #Xét đỉnh u

#Đỉnh u chưa duyệt

#Duyệt đô thị từ đỉnh u

graph, vertices = createAdjListGraph('dothi.txt')

bfs (graph)

#Tạo đồ thị từ tập