Câu hỏi:
13/10/2024 250Một máy bay đang bay ở độ cao \[12\] km, khi hạ cánh xuống mặt đất, đường đi của máy bay tạo với mặt đất một góc nghiêng \[\alpha .\] Nếu đường bay của máy bay dài \[320\] km thì góc nghiêng \[\alpha \] gần nhất với
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Ta mô hình hóa bài toán như hình vẽ trên.
Theo bài, máy bay đang ở độ cao \[12\] km nên \[AH = 12\] (km); đường bay từ \[A\] đến \[B\] của máy bay dài \[320\] km nên \[AB = 320\] (km).
Vì tam giác \[AHB\] vuông tại \[H\] nên \[\sin \alpha = \sin \widehat {ABH} = \frac{{AH}}{{AB}} = \frac{{12}}{{320}} = \frac{3}{{80}}.\]
Sử dụng máy tính cầm tay, chuyển máy tính về chế độ “độ”, sau đó ấn liên tiếp các phím
Ấn tiếp phím , ta thấy màn hình hiện lên kết quả: \[2^\circ 8'56.74''.\]
Khi làm tròn đến phút, ta được kết quả \[\alpha = 2^\circ 9'.\]
Vậy ta chọn phương án A.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
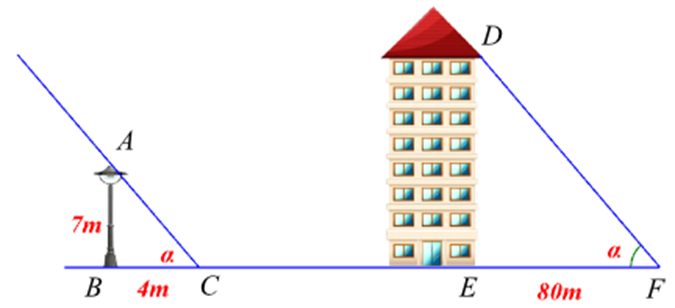
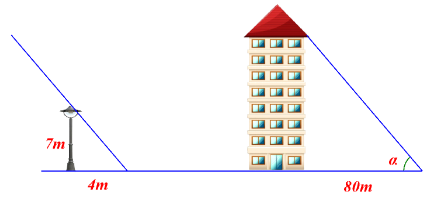
Giả sử bóng trên mặt đất của cột đèn và tia nắng mặt trời tạo nên một góc nghiêng \[\alpha .\]
Suy ra cùng lúc đó, bóng trên mặt đất của tòa nhà và tia nắng mặt trời cũng tạo nên một góc nghiêng \[\alpha .\]
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\tan \alpha = \frac{{AB}}{{BC}} = \frac{7}{4}\] (1)
Vì tam giác \[DEF\] vuông tại \[E\] nên \[\tan \alpha = \frac{{DE}}{{EF}} = \frac{{DE}}{{80}}\] (2)
Từ (1), (2), ta thu được \[\frac{{DE}}{{80}} = \frac{7}{4}.\]
Do đó \[DE = \frac{7}{4} \cdot 80 = 140\] (m).
Như vậy, chiều cao của tòa nhà là \[140\] m.
Vậy tòa nhà đó cao \[140:2 = 70\] (tầng).
Do đó ta chọn phương án C.
Lời giải
Đáp án đúng là: C
Vì \[\alpha ,\beta \] là hai góc phụ nhau nên \[\beta = 90^\circ - \alpha .\]
Theo định lí tỉ số lượng giác của hai góc phụ nhau, ta có:
\[\sin \alpha = \cos \left( {90^\circ - \alpha } \right) = \cos \beta ;\]
\[\tan \alpha = \cot \left( {90^\circ - \alpha } \right) = \cot \beta .\]
Vậy ta chọn phương án C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận