III. Vận dụng
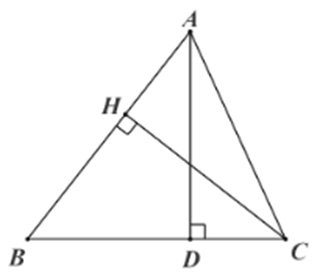
Cho tam giác \[ABC\] vuông tại \[A\] có \[AH\] là đường cao. Biết \[AB = 10\] cm, \[BH = 5\] cm. Tỉ số lượng giác \[\cos C\] bằng
A. \[\frac{{\sqrt 2 }}{2}.\]
B. \[\frac{1}{2}.\]
C. \[\frac{{\sqrt 3 }}{2}.\]
D. \[\sqrt 3 .\]
Quảng cáo
Trả lời:
Đáp án đúng là: C
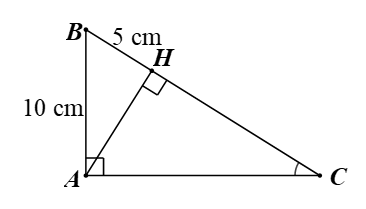
Tam giác \[ABC\] vuông tại \[A\] có: \[\widehat {B\,} + \widehat {C\,} = 90^\circ .\]
Do đó hai góc \(B\) và \(C\) phụ nhau nên \(\cos C = \sin B.\)
Tam giác \[ABC\] vuông tại \[A\] có \[AH\] là đường cao nên \[AH \bot BC\] tại \[H.\]
Xét tam giác \[ABH\] vuông tại\(H,\) theo định lí Pythagore, ta có: \(A{B^2} = A{H^2} + B{H^2}\)
Suy ra \(A{H^2} = A{B^2} - B{H^2} = {10^2} - {5^2} = 75.\) Do đó \(AH = \sqrt {75} = 5\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\)
Ta có \[\cos C = \sin B = \frac{{AH}}{{AB}} = \frac{{5\sqrt 3 }}{{10}} = \frac{{\sqrt 3 }}{2}.\]
Vậy ta chọn phương án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[10,069\] m.
B. \[10,07\] m.
C. \[10,06\] m.
D. \[10,7\] m.
Lời giải
Đáp án đúng là: B
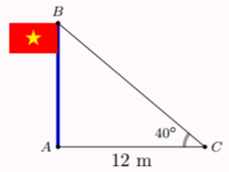
Vì tam giác \[ABC\] vuông tại \[A\] nên \[AB = AC.\tan C = 12.\tan 40^\circ \approx 10,07\] (m).
Do đó chiều cao \[AB\] của cột cờ khoảng \[10,07\] m.
Vậy ta chọn phương án B.
Câu 2
A. \[A\] m.
B. \[5\] m.
C. \[6\] m.
D. \[7\] m.
Lời giải
Đáp án đúng là: B
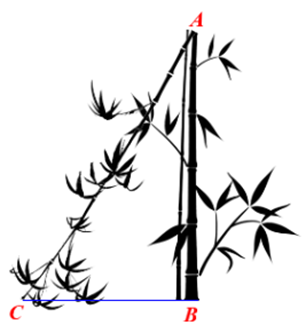
Ta mô hình hóa bài toán như hình vẽ bên.
Khoảng cách từ gốc cây đến điểm bị gãy là \[AB.\]
Khoảng cách từ điểm thân tre bị gãy đến ngọn cây là \[BC.\]
Khoảng cách từ ngọn cây chạm đất đến gốc là \[AC.\]
Đặt độ dài \(BC = x{\rm{\;(m)}}\,\,\left( {0 < x < 9} \right)\).
Suy ra: \(AB = 9 - x.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = BC \cdot \cos B\)
Suy ra \(9 - x = x \cdot \cos 32^\circ \)
\(9 - x \approx 0,85x\)
\(1,85x \approx 9\)
\[x \approx 4,9{\rm{\;(m)}}{\rm{.}}\]
Do đó điểm gãy cách gốc khoảng 4,9 m.
Vậy ta chọn phương án B.
Câu 3
D. \[c = a\tan B.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
B. \[HC = BC.\cos B.\]
D. \[HC = BC.\cot B.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[BC = \sqrt {39} \] cm; \[AC = 8\] cm.
B. \[BC = 8\] cm; \[AC = \sqrt {39} \] cm.
C. \[BC = 16\] cm; \[AC = \sqrt {39} \] cm.
D. \[BC = 4\] cm; \[AC = \frac{{\sqrt {39} }}{2}\] cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\sin C = \frac{{AB}}{{BC}} = \frac{3}{5}.\]
B. \[\cos C = \frac{{AC}}{{BC}} = \frac{4}{5}.\]
C. \[\tan B = \frac{{AC}}{{AB}} = \frac{4}{3}.\]
D. \[\cot B = \frac{{AB}}{{BC}} = \frac{3}{5}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\sin \alpha - \cos \alpha = 0\).
B. \(\cos \alpha - \cos \beta = 0\).
C. \(\tan \alpha - \cot \beta = 0\).
D. \(\tan \alpha \cdot \cot \beta = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.