Câu hỏi:

13/10/2024 204

Trong không gian \[Oxyz\] cho hình chóp \[S.ABCD\] có \[S\left( {0;0;\frac{{a\sqrt 3 }}{2}} \right),\]\[A\left( {\frac{a}{2};0;0} \right),\]\[B\left( { - \frac{a}{2};0;0} \right)\], \[C\left( { - \frac{a}{2};a;0} \right)\],\[D\left( {\frac{a}{2};a;0} \right)\] với \[a > 0\]. Tính góc giữa đường thẳng \[SD\] và mặt phẳng \[\left( {SAC} \right)\]. (Kết quả làm tròn đến hàng đơn vị của độ).

A. \[28^\circ \].

B. \[38^\circ \].

C. \[26^\circ \].

D. \[31^\circ \].

Xem lời giải

Câu hỏi trong đề: 20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 16. Công thức tính góc trong không gian có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: A

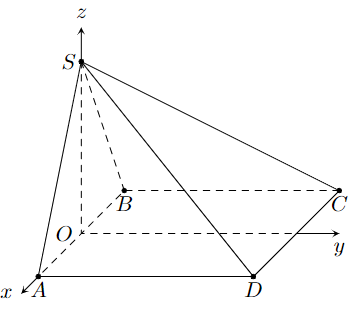
rong không gian O x y z cho hình chóp S . A B C D có S ( 0 ; 0 ; a √ 3 / 2 ) , A ( a 2 ; 0 ; 0 ) , B ( − a/ 2 ; 0 ; 0 ) , C ( − a/ 2 ; a ; 0 ) , D ( a 2 ; a ; 0 ) với a > 0 . Tính góc giữa đường thẳng S D và mặt phẳng ( S A C ) . (Kết quả làm tròn đến hàng đơn vị của độ). (ảnh 1)

Ta có: \[\overrightarrow {SD} = \left( {\frac{a}{2};a; - \frac{{a\sqrt 3 }}{2}} \right) = a\left( {\frac{1}{2};1; - \frac{{\sqrt 3 }}{2}} \right)\],

\[\overrightarrow {SA} = \left( {\frac{a}{2};0; - \frac{{a\sqrt 3 }}{2}} \right) = a\left( {\frac{1}{2};0; - \frac{{\sqrt 3 }}{2}} \right)\],

\[\overrightarrow {SC} = \left( { - \frac{a}{2};a; - \frac{{a\sqrt 3 }}{2}} \right) = a\left( { - \frac{1}{2};1; - \frac{{\sqrt 3 }}{2}} \right)\].

Vectơ pháp tuyến của mặt phẳng \[\left( {SAC} \right)\] là \[\overrightarrow n = \left[ {\overrightarrow {SA} ,\overrightarrow {SC} } \right]\].

Ta có: \[\overrightarrow n = \left[ {\overrightarrow {SA} ,\overrightarrow {SC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&{ - \frac{{\sqrt 3 }}{2}}\\1&{ - \frac{{\sqrt 3 }}{2}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}\\{ - \frac{{\sqrt 3 }}{2}}&{ - \frac{1}{2}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{\frac{1}{2}}&0\\{ - \frac{1}{2}}&1\end{array}} \right|} \right) = \left( {\frac{{\sqrt 3 }}{2};\frac{{\sqrt 3 }}{2};\frac{1}{2}} \right).\]

Ta có: \[\sin \left( {SD,\left( {SAC} \right)} \right) = \left| {\cos \left( {\overrightarrow {SD} ,{{\overrightarrow n }_{\left( {SAC} \right)}}} \right)} \right|\]

\[ = \frac{{\left| {\frac{{\sqrt 3 }}{2}.\frac{1}{2} + 1.\frac{{\sqrt 3 }}{2} + \left( { - \frac{{\sqrt 3 }}{2}} \right).\frac{1}{2}} \right|}}{{\sqrt {{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}} .\sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {1^2} + {{\left( { - \frac{{\sqrt 3 }}{2}} \right)}^2}} }}\]

\[ = \frac{{\sqrt {42} }}{{14}}.\]

Suy ra \[\widehat {\left( {SD,\left( {SAC} \right)} \right)} \approx 28^\circ .\]

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong hệ tọa độ \[Oxyz\], cho ba điểm \[M\left( {1;0;0} \right)\], \[N\left( {0;1;0} \right)\] và \[P\left( {0;0;1} \right)\]. Cosin của góc giữa hai mặt phẳng \[\left( {MNP} \right)\] và \[\left( {Oxy} \right)\] bằng

A. \[\frac{1}{{\sqrt 3 }}.\]

B. \[\frac{1}{{\sqrt 5 }}.\]

C. \[\frac{2}{{\sqrt 5 }}.\]

D. \[\frac{1}{3}.\]

Lời giải

Đáp án đúng là: A

Ta có: \[\overrightarrow {MN} = \left( { - 1;1;0} \right),\overrightarrow {MP} = \left( { - 1;0;1} \right),\]\[{\overrightarrow n _{\left( {Oxy} \right)}} = \left( {0;0;1} \right)\].

Suy ra \[{\overrightarrow n _{\left( {MNP} \right)}} = \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {\left| {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 1}\\1&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&1\\{ - 1}&0\end{array}} \right|} \right) = \left( {1;1;1} \right).\]

Suy ra \[\cos \left( {\left( {MNP} \right),\left( {Oxy} \right)} \right) = \left| {\cos \left( {{{\overrightarrow n }_{\left( {Oxy} \right)}},{{\overrightarrow n }_{\left( {MNP} \right)}}} \right)} \right| = \frac{1}{{\sqrt 3 }}.\]

Câu 2

Trong hệ tọa độ \[Oxyz\], cho mặt phẳng \[\left( P \right):2x - y - z - 3 = 0\] và \[\left( Q \right):x - z - 2 = 0\]. Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng

A. \[0^\circ.\]

B. \[90^\circ.\]

C. \[45^\circ.\]

D. \[30^\circ.\]

Lời giải

Đáp án đúng là: D

Ta có: \[{\overrightarrow n _{\left( P \right)}} = \left( {2; - 1; - 1} \right)\], \[{\overrightarrow n _{\left( Q \right)}} = \left( {1;0; - 1} \right)\].

Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng

\[\cos \left( {\left( P \right),\left( Q \right)} \right) = \cos \left| {{{\overrightarrow u }_{\left( P \right)}},{{\overrightarrow n }_{\left( Q \right)}}} \right|\]

\[ = \frac{{\left| {1.2 + 0.\left( { - 1} \right) + \left( { - 1} \right).\left( { - 1} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {0^2} + {{\left( { - 1} \right)}^2}} }} = \frac{3}{{2\sqrt 3 }} = \frac{{\sqrt 3 }}{2}.\]

Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng \[30^\circ .\]

Câu 3

III. Vận dụng

Trong không gian \[Oxyz\], cho mặt phẳng \[\left( P \right):3x + 4y + 5z + 2 = 0\] và đường thẳng \[d\] là giao tuyến của hai mặt phẳng \[\left( \alpha \right):x - 2y + 1 = 0\] và \[\left( \beta \right):x - 2y - 3z = 0\]. Hãy tính số đo góc \[\alpha \] giữa \[d\] và \[\left( P \right)\].

A. \[60^\circ.\]

B. \[90^\circ.\]

C. \[45^\circ.\]

D. \[30^\circ.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong không gian \[Oxyz\], cho hình chóp \[S.ABC\] có ba điểm \[S\left( {0;0;3} \right)\], \[A\left( {0;0;0} \right)\], \[B\left( {1;0;0} \right)\], \[C\left( {0;2;0} \right)\] và mặt phẳng \[\left( P \right):x + y + z - 3 = 0\]. Xét các mệnh đề sau:

a) Cosin góc giữa hai mặt phẳng \[\left( {SAB} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[0.\]

b) Cosin góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[\frac{2}{7}.\]

c) Cosin góc giữa hai mặt phẳng \[\left( {SBC} \right)\] và mặt phẳng \[\left( P \right)\] bằng \[\frac{{10\sqrt 3 }}{{21}}.\]

d) Góc giữa hai mặt phẳng \[\left( {SAC} \right)\] và mặt phẳng \[\left( {ABC} \right)\] bằng \[90^\circ .\]

Số mệnh đề đúng là

A. 1.

B. 2.

C. 3.

D. 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tìm tất cả các mặt phẳng \[\left( \alpha \right)\] chứa đường thẳng \[d:\frac{x}{1} = \frac{y}{{ - 1}} = \frac{z}{{ - 3}}\] và tạo với mặt phẳng \[\left( P \right):2x - z + 1 = 0\] góc \[45^\circ .\]

A. \[\left( \alpha \right):3x + z = 0.\]

B. \[\left( \alpha \right):x - y - 3z = 0.\]

C. \[\left( \alpha \right):x + 3z = 0.\]

D. \[\left( \alpha \right):3x + z = 0\] hoặc \[\left( \alpha \right):8x + 5y + z = 0.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong hệ tọa độ \[Oxyz\], cho hai đường thẳng \[{\Delta _1}\] và \[{\Delta _2}\] có vectơ chỉ phương lần lượt là \[\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right)\], \[\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\]. Khi đó, khẳng định nào sau đây là sai?

A. \[\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left| {\left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right|.\]

B. \[\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]

C. \[\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}.\]

D. \[\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)\] hoặc \[\left( {{\Delta _1},{\Delta _2}} \right) = 180^\circ - \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right).\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian \[Oxyz\], cho hai đường thẳng \[{\Delta _1}\] và \[{\Delta _2}\] có vectơ chỉ phương lần lượt là \[\overrightarrow {{u_1}} = \left( {{a_1};{b_1};{c_1}} \right)\], \[\overrightarrow {{u_2}} = \left( {{a_2};{b_2};{c_2}} \right)\]. Gọi \[\varphi \] là góc giữa hai đường thẳng \[{\Delta _1}\] và \[{\Delta _2}.\] Xét các khẳng định sau:

a) \[\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]

b) \[\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]

c) \[{\Delta _1} \bot {\Delta _2} \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2} = 0.\]

d) \[\sin \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}.\]

Số khẳng định đúng trong các khẳng định trên là

A. 1.

B. 0.

C. 2.

D. 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong hệ tọa độ \[Oxyz\], cho ba điểm \[M\left( {1;0;0} \right)\], \[N\left( {0;1;0} \right)\] và \[P\left( {0;0;1} \right)\]. Cosin của góc giữa hai mặt phẳng \[\left( {MNP} \right)\] và \[\left( {Oxy} \right)\] bằng

Trong hệ tọa độ \[Oxyz\], cho mặt phẳng \[\left( P \right):2x - y - z - 3 = 0\] và \[\left( Q \right):x - z - 2 = 0\]. Góc giữa hai mặt phẳng \[\left( P \right)\] và \[\left( Q \right)\] bằng

Tìm tất cả các mặt phẳng \[\left( \alpha \right)\] chứa đường thẳng \[d:\frac{x}{1} = \frac{y}{{ - 1}} = \frac{z}{{ - 3}}\] và tạo với mặt phẳng \[\left( P \right):2x - z + 1 = 0\] góc \[45^\circ .\]

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu