Trong không gian \[Oxyz\], cho điểm \[H\left( {1;2; - 2} \right)\]. Mặt phẳng \[\left( \alpha \right)\] đi qua \[H\] và cắt các trục \[Ox,Oy,Oz\] tại \[A,B,C\] sao cho \[H\] là trực tâm của tam giác \[ABC\]. Viết phương trình mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng \[\left( \alpha \right)\].
A. \[{x^2} + {y^2} + {z^2} = 81.\]
B. \[{x^2} + {y^2} + {z^2} = 1.\]
C. \[{x^2} + {y^2} + {z^2} = 9.\]
D. \[{x^2} + {y^2} + {z^2} = 25.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
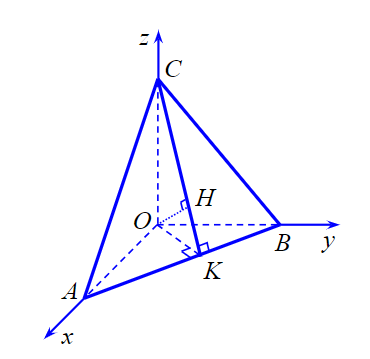
Ta có
\[H\] là trực tâm của tam giác \[ABC\], suy ra \[OH \bot \left( {ABC} \right)\].
Thật vậy:
\[\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\end{array} \right. \Rightarrow OC \bot AB\] (1)
Mà \[CH \bot AB\] (vì \[H\] là trực tâm tam giác \[ABC\]) (2).
Từ (1) và (2) suy ra \[AB \bot \left( {OHC} \right)\]\[ \Rightarrow AB \bot OH\].
Tương tự, ta suy ra \[BC \bot \left( {OAH} \right)\]\[ \Rightarrow BC \bot OH.\]
Từ đây suy ra \[OH \bot \left( {ABC} \right).\]
Khi đó, mặt cầu tâm \[O\] tiếp xúc mặt phẳng \[\left( {ABC} \right)\] có bán kính \[R = OH = 3.\]
Vậy mặt cầu tâm \[O\] và tiếp xúc với mặt phẳng \[\left( \alpha \right)\] là \[{x^2} + {y^2} + {z^2} = 9.\]
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[{x^2} + {y^2} + {z^2} - 2x = 0.\]
B. \[{x^2} + {y^2} - {z^2} + 2x - y + 1 = 0.\]
C. \[2{x^2} + {y^2} = {\left( {x + y} \right)^2} - {z^2} + 2x + 1.\]
D. \[{\left( {x + y} \right)^2} = 2xy - {z^2} - 1.\]
Lời giải
Đáp án đúng là: A
Phương trình mặt cầu có dạng
\[{x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\] với \[d = {a^2} + {b^2} + {c^2} - {R^2}.\]
Xét các đáp án, chỉ có đáp án A thỏa mãn, đồng thời ta có thể viết lại như sau:
\[{x^2} + {y^2} + {z^2} - 2x = 0\] hay \[{\left( {x - 1} \right)^2} + {y^2} + {z^2} = 1\].
Câu 2
A. \[{x^2} + {y^2} + {z^2} + 4x - 2y + 2z = 0.\]
B. \[{x^2} + {y^2} + {z^2} - 4x - 2y + 2z = 0.\]
C. \[{x^2} + {y^2} + {z^2} - 2x - y + z - 6 = 0.\]
D. \[{x^2} + {y^2} + {z^2} - 4x - 2y + 2z + 6 = 0.\]
Lời giải
Đáp án đúng là: A
Tâm \[I\] của mặt cầu là trung điểm của \[AB\] do đó \[I\left( {2;1; - 1} \right)\].
Ta có: \[R = IA = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {1 - 0} \right)}^2} + {{\left( { - 1 - \left( { - 3} \right)} \right)}^2}} = \sqrt 6 .\]
Vậy phương trình mặt cầu đường kính \[AB\] là
\[{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 6\] hay \[{x^2} + {y^2} + {z^2} - 4x - 2y + 2z = 0.\]
Câu 3
A. \[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{\sqrt {213} }}{3}.\]
B. \[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{71}}{3}.\]
C. \[{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 3} \right)^2} = \frac{{\sqrt {213} }}{3}.\]
D. \[{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 3} \right)^2} = \frac{{71}}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[{\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} + {\left( {z - {z_0}} \right)^2} = {R^2}.\]
B. \[\left( {x - {x_0}} \right) + \left( {y - {y_0}} \right) + \left( {z - {z_0}} \right) = R.\]
C. \[\left( {x - {x_0}} \right) + \left( {y - {y_0}} \right) + \left( {z - {z_0}} \right) = {R^2}.\]
D. \[{\left( {x - {x_0}} \right)^2} - {\left( {y - {y_0}} \right)^2} - {\left( {z - {z_0}} \right)^2} = {R^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\left( {9;18; - 27} \right).\]
B. \[\left( { - 3; - 6;9} \right).\]
C. \[\left( {3;6; - 9} \right).\]
D. \[\left( { - 9; - 18;27} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[{x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0.\]
B. \[{x^2} + {y^2} + {z^2} + 4x - 2y + 2z + 6 = 0.\]
C. \[{x^2} + {y^2} + {z^2} + 2x - 6y + 4z + 14 = 0.\]
D. \[{x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo