Câu hỏi:
14/10/2024 4,393Một li rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc cốc thành 2 phần bằng nhau) là một đường parabol.
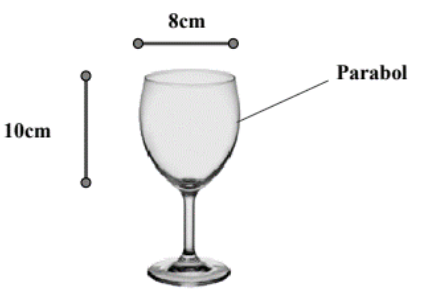
Thể tích tối đa mà cốc có thể chứa được là (làm tròn kết quả đến hai chữ số thập phân).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Gắn phần miệng li đựng nước vào hệ trục tọa độ, với đỉnh trùng với gốc tọa độ.
Lúc này, ta được parabol đi qua các điểm (0; 0), (−4; 10); (4; 10).
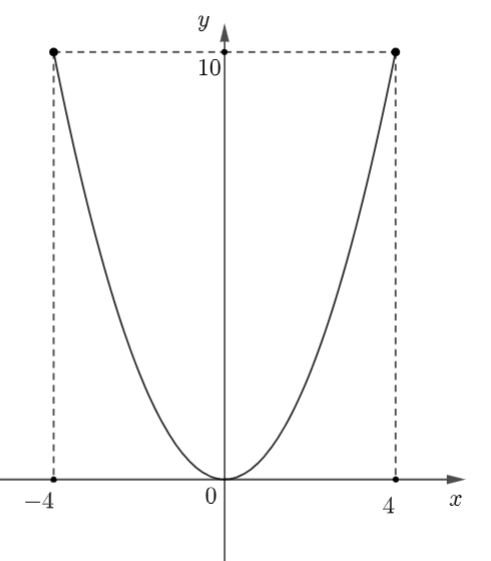
Gọi phương trình parabol là: \[y = a{x^2} + bx + c\] \[\left( {a \ne 0} \right)\].
Ta có: \[\left\{ \begin{array}{l}c = 0\\16a - 4b + c = 10\\16a + 4b + c = 10\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 0\\a = \frac{5}{8}\\b = 0\end{array} \right.\].
Vậy \[y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y \Leftrightarrow x = \sqrt {\frac{8}{5}y} \]
Thể tích tối đa mà cốc có thể chứa nước là
\[V = \pi {\int\limits_0^{10} {\left( {\sqrt {\frac{8}{5}} y} \right)} ^2}dy = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)dy = \left. {\pi \frac{4}{5}{y^2}} \right|_0^{10}} = 80\pi \approx 251,33\] cm3.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Ta có: \[V = \pi \int\limits_0^1 {{{\left( {{x^2} - 2x} \right)}^2}dx = } \pi \int\limits_0^1 {\left( {{x^4} - 4{x^3} + 4{x^2}} \right)dx} \]
\[ = \left. {\pi \left( {\frac{{{x^5}}}{5} - {x^4} + \frac{4}{3}{x^3}} \right)} \right|_0^1 = \frac{{8\pi }}{{15}}.\]
Lời giải
Đáp án đúng là: A
Xét \[y = \left\{ \begin{array}{l} - x,{\rm{ }}x \le 1\\x - 2{\rm{, }}x > 1\end{array} \right.\], ta có:
\[\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x - 2} \right) = - 1\]; \[\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x} \right) = - 1\] và \[y\left( 1 \right) = - 1\].
Do đó hàm số liên tục tại \[x = 1.\]
Diện tích hình phẳng cần tính là:
\[S = \int\limits_0^1 {\left( {\frac{{10}}{3}x - {x^2} + x} \right)dx + } \int\limits_1^3 {\left( {\frac{{10}}{3}x - {x^2} - x + 2} \right)dx} \]
\[ = \int\limits_0^1 {\left( {\frac{{13}}{3}x - {x^2}} \right)dx + } \int\limits_1^3 {\left( {\frac{7}{3}x - {x^2} + 2} \right)dx} \]
\[ = \left. {\left( {\frac{{13}}{6}{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 + \left. {\left( {\frac{7}{6}{x^2} - \frac{{{x^3}}}{3} + 2x} \right)} \right|_1^3 = \frac{{13}}{2} = 6,5.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo