Cho đường tròn \[\left( {O;3{\rm{\;cm}}} \right)\] và điểm \[A \in \left( O \right).\] Đường thẳng \[d\] vuông góc với \[OA\] tại trung điểm của \[OA\] cắt đường tròn \[\left( O \right)\] tại \[B\] và \[C.\] Kết luận nào sau đây đúng nhất?
A. Đường thẳng \[d\] là trục đối xứng của đoạn \[OA.\]
B. Tam giác \[OAB\] đều.
C. \[BC = 3\sqrt 3 \] cm.
D. Cả A, B, C đều đúng.
Quảng cáo
Trả lời:
Đáp án đúng là: D
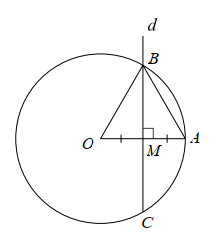
Gọi \[M\] là trung điểm \[OA.\]
⦁ Vì đường thẳng \[d\] vuông góc với \[OA\] tại trung điểm \[M\] của \[OA\] nên đường thẳng \[d\] là đường trung trực của đoạn \[OA.\]
Do đó đường thẳng \[d\] là trục đối xứng của đoạn \[OA.\] Vì vậy phương án A đúng.
⦁ Xét \[\Delta OBM\] và \[\Delta ABM,\] có:
\[\widehat {BMO} = \widehat {BMA} = 90^\circ ;\] \[BM\] là cạnh chung; \[OM = AM\] (do \[M\] là trung điểm \[OA\])
Do đó \[\Delta OBM = \Delta ABM\] (c.g.c)
Suy ra \[OB = AB\] (cặp cạnh tương ứng)
Mà tam giác \[OAB\] cân tại \(O\) (do \[OA = OB)\] nên tam giác \[OAB\] đều. Vì vậy phương án B đúng.
⦁ Ta có \[OA = OB = 3{\rm{\;(cm)}}\]. Vì \[M\] là trung điểm \[OA\] nên \[OM = \frac{{OA}}{2} = \frac{3}{2}{\rm{\;(cm)}}{\rm{.}}\]
Áp dụng định lí Pythagore cho tam giác \[OBM\] vuông tại \[M,\] ta được: \[O{B^2} = B{M^2} + O{M^2}\]
Suy ra \[B{M^2} = O{B^2} - O{M^2} = {3^2} - {\left( {\frac{3}{2}} \right)^2} = \frac{{27}}{4}\]. Do đó \[BM = \frac{{3\sqrt 3 }}{2}{\rm{\;(cm)}}{\rm{.}}\]
Vì đường thẳng \[OA\] là trục đối xứng của \[\left( O \right)\] nên điểm đối xứng với điểm \[B\] qua đường thẳng \[OA\] phải vừa thuộc \[\left( O \right)\], vừa thuộc đường vuông góc hạ từ \[B\] xuống \[OA.\]
Tức là \[M\] là trung điểm của \(BC\) nên \[BC = 2BM = 2 \cdot \frac{{3\sqrt 3 }}{2} = 3\sqrt 3 {\rm{\;(cm)}}{\rm{.}}\] Vì vậy phương án C đúng.
Vậy ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[12{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: D
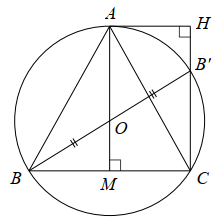
Vì \[B'\] là điểm đối xứng với \[B\] qua \[O\] và \(B \in \left( O \right)\) nên \[B' \in \left( O \right).\]
Suy ra \[OB = OB' = R\] và \(BB' = 2R.\)
Mà \[C \in \left( O \right)\] nên \[R = OC = OB = OB' = \frac{{BB'}}{2}.\]
Tam giác \[BB'C\] có \[OC\] là đường trung tuyến ứng với cạnh \(BB'\) và \[OC = \frac{{BB'}}{2}\] nên tam giác \[BB'C\] vuông tại \[C.\]
Tứ giác \[AHCM,\] có: \[\widehat {AMC} = \widehat {AHC} = \widehat {HCM} = 90^\circ \] nên tứ giác \[AHCM\] là hình chữ nhật.
Tam giác \[ABC\] cân tại \[A\] có \[AM\] là đường cao nên \[AM\] cũng là đường trung tuyến của tam giác. Do đó \[M\] là trung điểm \[BC.\] Vì vậy \[MC = \frac{{BC}}{2} = \frac{6}{2} = 3{\rm{\;(cm)}}{\rm{.}}\]
Vậy chu vi hình chữ nhật \[AHCM\] bằng \[2 \cdot \left( {AM + MC} \right) = 2 \cdot \left( {4 + 3} \right) = 14{\rm{\;(cm)}}{\rm{.}}\]
Do đó ta chọn phương án D.
Câu 2
A. \[\Delta ABC\] có \[AB = 2BC.\]
Lời giải
Đáp án đúng là: C
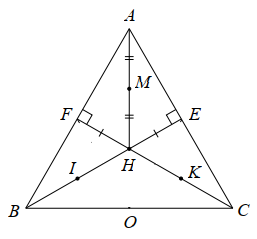
Xét \[\Delta ABC\] cân tại \[A\] có hai đường cao \[BE\] và \[CF\] cắt nhau tại \[H\] nên \[H\] là trực tâm của \[\Delta ABC.\]
Khi đó \[AH\] là đường cao thứ ba của \[\Delta ABC.\]
Mà \[\Delta ABC\] cân tại \[A\] nên đường cao \[AH\] cũng là đường phân giác của \[\Delta ABC.\]
Xét \[\Delta AFH\] và \[\Delta AEH,\] có:
\[\widehat {AFH} = \widehat {AEH} = 90^\circ ;\]
\[AH\] là cạnh chung;
\[\widehat {FAH} = \widehat {EAH}\] (do \[AH\] là đường phân giác của \[\widehat {FAE}\]).
Do đó \[\Delta AFH = \Delta AEH\] (cạnh huyền – góc nhọn)
Suy ra \[HF = HE\] (cặp cạnh tương ứng).
Mà \[HI = HE,\,\,HK = HF\] nên \[HE = HI = HF = HK.\]
Vậy bốn điểm \[E,F,I,K\] cùng nằm trên đường tròn tâm \[H\] bán kính \[HE.\]
Tam giác \[AEH\] vuông tại \[E\] có \[EM\] là đường trung tuyến ứng với cạnh huyền \(AH\) nên \(EM = MA = MH = \frac{1}{2}AH\).
Do đó tam giác \[HME\] cân tại \[M.\]
Để điểm \[M\] thuộc đường tròn đi qua bốn điểm \[E,F,I,K\] thì \[HM = HE.\]
Mà tam giác \[HME\] cân tại \[M\] nên lúc này, tam giác \[HME\] là tam giác đều.
Suy ra \[\widehat {MHE} = 60^\circ .\]
Tam giác \[AEH\] vuông tại \[E\] có \[\widehat {AHE} + \widehat {HAE} = 90^\circ \]
Suy ra \[\widehat {HAE} = 90^\circ - \widehat {AHE} = 90^\circ - 60^\circ = 30^\circ .\]
Lại có \[AH\] là đường phân giác của \[\Delta ABC\] nên \[\widehat {BAC} = 2\widehat {HAE} = 2 \cdot 30^\circ = 60^\circ .\]
Khi này, \[\Delta ABC\] cân tại \[A\] có \[\widehat {BAC} = 60^\circ \] nên \[\Delta ABC\] là tam giác đều.
Vậy \[\Delta ABC\] đều thì điểm \[M\] thuộc đường tròn đi qua bốn điểm \[E,F,I,K.\]
Do đó ta chọn phương án C.
Câu 3
A. \[4\sqrt 3 {\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Hình vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(4{\rm{\;cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Điểm \[K\] nằm trong đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
B. Điểm \[K\] nằm ngoài đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
C. Điểm \[K\] nằm trên đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
D. Điểm \[K\] thuộc đường tròn \[\left( {O;5{\rm{\;cm}}} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.