Câu hỏi:
12/11/2024 549Hai tiếp tuyến tại \(B\) và \(C\) của đường tròn \(\left( O \right)\) cắt nhau tại \(A.\) Biết \(OB = 3{\rm{\;cm}},\,\,OA = 5{\rm{\;cm}}{\rm{.}}\) Khẳng định nào sau đây là sai?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
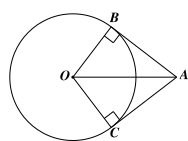
Vì \(AB,\,\,AC\) là tiếp tuyến của đường tròn \(\left( O \right)\) lần lượt tại \(B\) nên \(AB \bot OB\).
Xét \(\Delta OAB\) vuông tại \(B,\) ta có: \(O{A^2} = A{B^2} + O{B^2}\) (định lí Pythagore)
Suy ra \(A{B^2} = O{A^2} - O{B^2} = {5^2} - {3^2} = 16.\) Do đó \(AB = 4{\rm{\;cm}}.\)
Trong \(\Delta OAB\) vuông tại \(B,\) ta cũng có: \({\rm{sin}}\widehat {OAB} = \frac{{OB}}{{OA}} = \frac{3}{5}.\)
Xét \(\Delta OAC\) vuông tại \(C,\) ta cũng có: \({\rm{tan}}\widehat {COA} = \frac{{AC}}{{OC}} = \frac{4}{3}.\)
Hai tiếp tuyến \(B\) và \(C\) của đường tròn \(\left( O \right)\) cắt nhau tại \(A\) nên:
⦁ \[AC = AB = 4{\rm{\;cm;}}\]
⦁ \(AO\) là tia phân giác của \(\widehat {BAC}\) nên \(\widehat {BAO} = \widehat {CAO}.\)
Như vậy, phương án D là khẳng định sai. Ta chọn phương án D.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
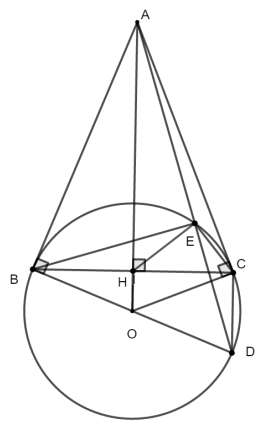
Ta có \[D\] đối xứng với \[B\] qua \[O.\] Suy ra \[O\] là trung điểm \[BD.\] Do đó \[BD\] là đường kính của đường tròn \[\left( O \right).\]
Tam giác \[BED\] có \[EO\] là đường trung tuyến và \[EO = \frac{{BD}}{2}\] nên tam giác \[BED\] vuông tại \[E.\]
Ta có \[AB\] là tiếp tuyến của đường tròn \[\left( O \right)\] tại \(B\) nên \[AB \bot BD.\]
Xét \[\Delta BED\] và \[\Delta ABD,\] có:
\[\widehat {BED} = \widehat {ABD} = 90^\circ \] và \[\widehat {BDE}\] là góc chung.
Do đó (g.g)
Suy ra \[\frac{{DE}}{{DB}} = \frac{{BE}}{{AB}}\] hay \[\frac{{DE}}{{BE}} = \frac{{DB}}{{AB}}.\]
Vậy ta chọn phương án D.
Lời giải
Đáp án đúng là: A
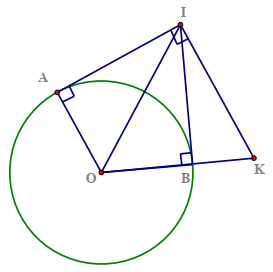
Vì đường tròn \[\left( O \right)\] có \[IA,IB\] là hai tiếp tuyến cắt nhau tại \[I\] nên \[\widehat {AOI} = \widehat {KOI}.\]
Lại có \[OA\,{\rm{//}}\,KI\] (vì cùng vuông góc với \[AI\]) nên \[\widehat {AOI} = \widehat {KIO}\] (cặp góc so le trong)
Do đó \[\widehat {KOI} = \widehat {KIO}.\]
Vì vậy tam giác \[KOI\] cân tại \[K.\]
Vậy ta chọn phương án A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1