II. Thông hiểu
Cho hình vẽ dưới đây biết \(AB,\,\,CB\) là hai tiếp tuyến của đường tròn \(\left( D \right).\)
![Cho hình vẽ dưới đây biết A B , C B là hai tiếp tuyến của đường tròn ( D ) .Giá trị của \[x\] bằng (ảnh 1)](https://video.vietjack.com/upload2/images/1731473440/1731474154-image5.png)
Giá trị của \[x\] bằng
A. \[x = \frac{3}{2}.\]
B. \[x = 6.\]
C. \[x = 24.\]
D. \[x = 96.\]
Quảng cáo
Trả lời:
Đáp án đúng là: B
Quan sát hình vẽ, ta thấy \[BA,BC\] là hai tiếp tuyến của đường tròn \[\left( D \right).\]
Áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[BA = BC.\]
Tức là, \[4x - 9 = 15\]
\[4x = 24\]
\[x = 6.\]
Vậy ta chọn phương án B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Chỉ (i) đúng.
B. Chỉ (ii) đúng.
C. Cả (i) và (ii) đều đúng.
D. Cả (i) và (ii) đều sai.
Lời giải
Đáp án đúng là: C
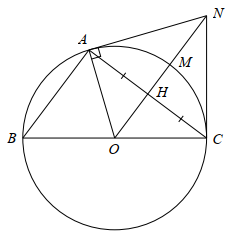
⦁ Đường tròn \[\left( O \right)\] có \[OA = OC = R\] nên tam giác \[OAC\] cân tại \[O.\]
Tam giác \[OAC\] cân tại \[O\] có \[OH\] là đường trung tuyến nên \[OH\] cũng là đường cao của tam giác, do đó \[OH \bot AC\] hay \[\widehat {OHA} = 90^\circ .\]
Vì \[AN\] là tiếp tuyến của đường tròn \[\left( O \right)\] nên \[OA \bot AN\] hay \[\widehat {OAN} = 90^\circ .\]
Xét \[\Delta OHA\] và \[\Delta OAN,\] có:
\[\widehat {OHA} = \widehat {OAN} = 90^\circ ;\] \[\widehat {AON}\] là góc chung.
Do đó (g.g). Suy ra \[\frac{{OH}}{{OA}} = \frac{{OA}}{{ON}}.\]
Vì vậy \[OH \cdot ON = O{A^2} = {R^2}.\] Do đó khẳng định (i) là đúng.
⦁ Tam giác \[OAC\] cân tại \[O\] có \[OH\] là đường trung tuyến nên \[OH\] cũng là đường phân giác của tam giác, do đó \[\widehat {AOH} = \widehat {COH}.\]
Xét \[\Delta AON\] và \[\Delta CON,\] có:
\[OA = OC = R;\] \[\widehat {AON} = \widehat {CON};\] \[ON\] là cạnh chung.
Do đó \[\Delta AON = \Delta CON\] (c.g.c).
Suy ra \[\widehat {OAN} = \widehat {OCN}.\] Nên \[\widehat {OCN} = 90^\circ .\]
Vì vậy \[OC \bot CN\] tại \[C\] hay \[CN\] là tiếp tuyến của \[\left( O \right).\] Do đó khẳng định (ii) là đúng.
Vậy ta chọn phương án C.
Câu 2
A. \[BM = 2{\rm{\;cm}}.\]
B. \[BM = 6{\rm{\;cm}}.\]
C. \[BM = 8{\rm{\;cm}}.\]
D. \[BM = 4{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: D
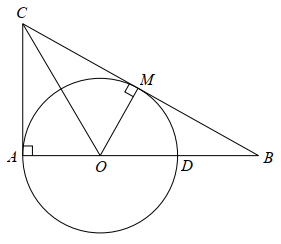
Vì \[AC\] là tiếp tuyến của đường tròn \[\left( O \right)\] nên \[AC \bot AO\] tại \[A.\]
Áp dụng định lí Pythagore cho tam giác \[ABC\] vuông tại \[A,\] ta được:
\[B{C^2} = A{B^2} + A{C^2} = {8^2} + {6^2} = 100.\] Suy ra \[BC = 10{\rm{\;(cm)}}{\rm{.}}\]
Vì \[AC,\,\,CM\] là hai tiếp tuyến của đường tròn \[\left( O \right)\] nên áp dụng tính chất hai tiếp tuyến cắt nhau, ta được \[CM = CA = 6{\rm{\;(cm)}}{\rm{.}}\]
Ta có \[BM = BC - CM = 10 - 6 = 4{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 3
A. \[11,137{\rm{\;km}}.\]
B. \[128,000{\rm{\;km}}.\]
C. \[11,33{\rm{\;km}}.\]
D. \[11,314{\rm{\;km}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Tam giác \[KOI\] cân tại \[K.\]
B. Tam giác \[KOI\] cân tại \[O.\]
C. Tam giác \[KOI\] cân tại \[I.\]
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[15{\rm{\;cm}}.\]
B. \[12\sqrt 3 {\rm{\;cm}}.\]
C. \[18{\rm{\;cm}}.\]
D. \[6\sqrt 3 {\rm{\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[OA \bot BC.\]
B. \[OA\] là đường trung trực của đoạn \[BC.\]
C. \[AB = AC.\]
D. \[OA \bot BC\] tại trung điểm của \[OA.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[d\] là tiếp tuyến của \[\left( O \right).\]
B. \[d\] cắt \[\left( O \right)\] tại hai điểm phân biệt.
C. \[d\] tiếp xúc với \[\left( O \right)\] tại \[O.\]
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.