Câu hỏi:
16/11/2024 699Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (như hình vẽ).
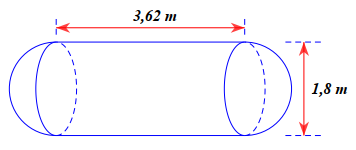
Thể tích của bồn chứa xăng là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Quan sát hình vẽ, ta thấy bán kính hình trụ bằng bán kính hai nửa hình cầu.
Bán kính hình cầu là: \[R = \frac{{1,8}}{2} = 0,9{\rm{\;(m)}}{\rm{.}}\]
Thể tích phần hình trụ là: \[{V_1} = \pi {R^2}h = \pi \cdot 0,{9^2} \cdot 3,62 = 2,9322\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Thể tích hai nửa hình cầu hay thể tích của hình cầu là:
\[{V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot 0,{9^3} = 0,972\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Thể tích của bồn chứa xăng là:
\[V = {V_1} + {V_2} = 2,9322\pi + 0,972\pi = 3,9042\pi {\rm{\;(}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Do đó thể tích của bồn chứa xăng là \[3,9042\pi \,\,{{\rm{m}}^3}.\]
Vậy ta chọn phương án D.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Ta thấy thể tích của viên bi bị bạn An đã bỏ vào lọ thủy tinh bằng thể tích của phần nước trong lọ thủy tinh dâng lên thêm \[2,25{\rm{\;cm}}.\]
Bán kính của lọ thủy tinh là: \[r = \frac{8}{2} = 4{\rm{\;(cm)}}{\rm{.}}\]
Thể tích phần nước trong lọ thủy tinh dâng lên thêm \[2,25{\rm{\;cm}}\] là:
\[V = \pi {r^2}h = \pi \cdot {4^2} \cdot 2,25 = 36\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Suy ra thể tích của viên bi bị bạn An đã bỏ vào lọ thủy tinh bằng \[36\pi {\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Gọi \(R{\rm{\;(cm)}}\) là bán kính của viên bi đặc hình cầu.
Thể tích của viên bi đó là: \(V = \frac{4}{3}\pi {R^3}{\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\)
Khi đó, ta có: \[\frac{4}{3}\pi {R^3} = 36\pi \]
Suy ra \[{R^3} = \frac{{36\pi }}{{\frac{4}{3}\pi }} = 27\] nên \[R = \sqrt[3]{{27}} = 3{\rm{\;(cm)}}{\rm{.}}\]
Do đó bán kính của viên bi bị bạn An đã bỏ vào lọ thủy tinh là \[3{\rm{\;cm}}.\]
Vậy ta chọn phương án A.
Lời giải
Đáp án đúng là: B
Dung tích của bể chứa là:
\[V = \frac{4}{3}\pi {R^3} \approx \frac{4}{3} \cdot 3,14 \cdot {6^3} = 904,320{\rm{\;(}}{{\rm{m}}^3}{\rm{)}} = 904\,\,320{\rm{\;(d}}{{\rm{m}}^3}{\rm{)}} = 904\,\,320\,\,(l).\]
Số lít nước người ta đã dự tính mức bình quân mỗi người dùng trong một ngày là:
\[904\,\,320:6\,\,520 \approx 139{\rm{\;(}}l{\rm{)}}{\rm{.}}\]
Do đó người ta đã dự tính mức bình quân mỗi người dùng \[139\] lít nước trong một ngày.
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1
-
Chuyên đề 8: Hình học (có đáp án)