Cho đường tròn 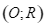 và điểm
và điểm  nằm ngoài đường tròn
nằm ngoài đường tròn 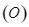 sao cho
sao cho 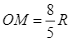 . Từ
. Từ  vẽ hai tiếp tuyến
vẽ hai tiếp tuyến 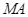 và
và 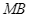 của đường tròn
của đường tròn 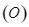 (với
(với 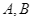 là hai tiếp điểm), đường thẳng
là hai tiếp điểm), đường thẳng 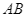 cắt
cắt 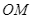 tại
tại 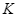 .
Kẻ đường kính
.
Kẻ đường kính 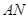 của đường tròn
của đường tròn 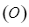 . Kẻ
. Kẻ 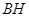 vuông góc với
vuông góc với 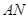 tại
tại 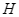 .
Cho
.
Cho 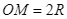 , tính diện tích hình quạt giới hạn bởi bán kính
, tính diện tích hình quạt giới hạn bởi bán kính 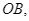
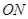 và cung nhỏ
và cung nhỏ 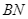 theo
theo 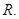
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
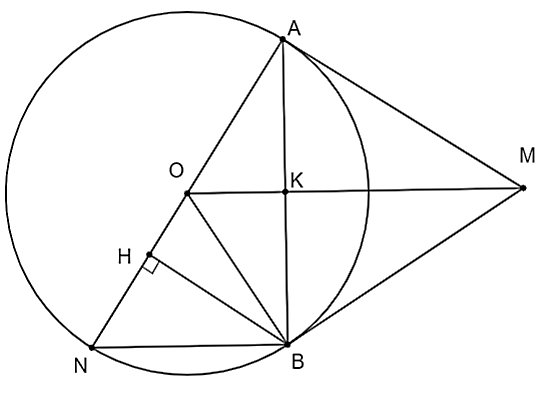
Xét ![]() vuông tại
vuông tại ![]() có:
có: ![]() suy ra
suy ra ![]()
Do ![]() và
và ![]() là hai tiếp tuyến của đường tròn
là hai tiếp tuyến của đường tròn ![]() nên
nên ![]() là tia phân giác góc
là tia phân giác góc ![]() (tính chất hai tiếp tuyến cắt nhau).
(tính chất hai tiếp tuyến cắt nhau).
Suy ra ![]() .
.
Do đó, ![]() nên
nên ![]() .
.
Diện tích hình quạt giới hạn bởi bán kính ![]()
![]() và cung nhỏ
và cung nhỏ ![]() là:
là:
![]() (đvdt).
(đvdt).
Vậy diện tích hình quạt giới hạn bởi bán kính ![]()
![]() và cung nhỏ
và cung nhỏ ![]() là
là ![]() (đvdt).
(đvdt).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi ![]() là số học sinh của lớp 9A,
là số học sinh của lớp 9A, ![]() là số học sinh của lớp 9B
là số học sinh của lớp 9B ![]() .
.
Theo đề bài, tổng số học sinh hai lớp là ![]() học sinh nên ta có phương trình
học sinh nên ta có phương trình ![]()
Lớp 9A góp được số giấy báo cũ là ![]() .
.
Lớp 9B góp được số giấy báo cũ là ![]() .
.
Mà lớp 9B góp nhiều hơn lớp 9A ![]() giấy báo cũ nên ta có phương trình:
giấy báo cũ nên ta có phương trình:
![]() suy ra
suy ra ![]() hay
hay ![]() .
.
Từ (1) và (2) ta có hệ phương trình: 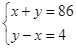 .
.
Cộng theo vế hai phương trình ta được ![]() , suy ra
, suy ra ![]() (TM).
(TM).
Thay ![]() vào phương trình (1), ta được
vào phương trình (1), ta được ![]() , suy ra
, suy ra ![]() (TM).
(TM).
Vậy lớp 9A có ![]() học sinh, lớp 9B có
học sinh, lớp 9B có ![]() học sinh.
học sinh.
Lời giải
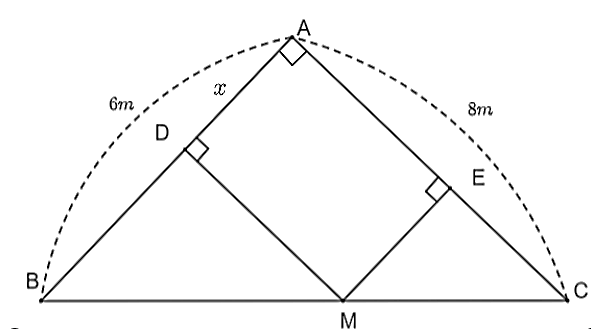
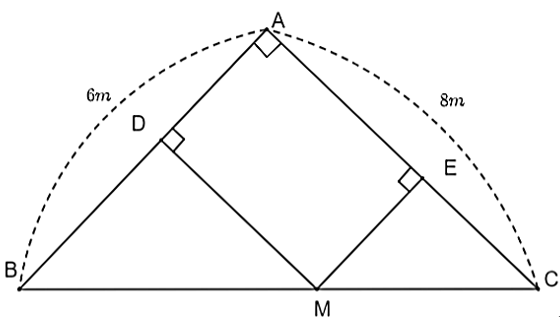
Đặt \[AD = x\,\,\left( {x > 0} \right)\].
Ta có tứ giác \[ADME\] có \[\widehat {ADE} = \widehat {DAE} = \widehat {AED} = 90^\circ \] nên \[ADME\] là hình chữ nhật. Do đó, \[AD = EM = x.\]
Xét \[\Delta ABC\] và \[\Delta ECM\] có:
\(\widehat A = \widehat {MEC} = 90^\circ \,;\,\,\widehat C\) chung.
Do đó (g.g)
Suy ra \[\frac{{EM}}{{AB}} = \frac{{CE}}{{CA}}\] hay \[\frac{x}{6} = \frac{{CE}}{8}\] suy ra \[CE = \frac{4}{3}x\].
Ta có \[AE = AC - EC = 8 - \frac{4}{3}x\].
Diện tích hình chữ nhật \[ADME\] là:
\[{S_{ADME}} = AD.AE = x\left( {8 - \frac{4}{3}x} \right)\].
Ta có: \[x\left( {8 - \frac{4}{3}x} \right) = - \frac{4}{3}{x^2} + 8x = - \frac{4}{3}\left( {{x^2} - 6x} \right)\]
\[ = - \frac{4}{3}\left( {{x^2} - 6x + 9} \right) + 12\]
\[ = - \frac{4}{3}{\left( {x - 3} \right)^2} + 12\].
Vì \[{\left( {x - 3} \right)^2} \ge 0\] với mọi \(x \in \mathbb{R}\) nên \[ - \frac{4}{3}{\left( {x - 3} \right)^2} \le 0\] với mọi \(x \in \mathbb{R}\).
Do đó \[ - \frac{4}{3}{\left( {x - 3} \right)^2} + 12 \le 12\] với mọi \(x \in \mathbb{R}\).
Dấu “=” xảy ra khi \[x - 3 = 0\] khi \[x = 3.\]
Khi đó \[D\] là trung điểm của \[AB\].
Suy ra \[M\] là trung điểm của \[BC\].
Do đó, diện tích lớn nhất của \[ADME\] bằng \[{\rm{12 }}{{\rm{m}}^{\rm{2}}}\] khi \[M\] là trung điểm của \[BC\].
Vậy diện tích ao cá lớn nhất mà người đó có thể đào là \[{\rm{12 }}{{\rm{m}}^{\rm{2}}}\] khi \[M\] là trung điểm của \[BC\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.