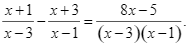Cho biểu thức \[A = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\] và \[B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\].
a) Tìm điều kiện xác định của biểu thức \[A\] và \[B.\]
b) Tính giá trị của biểu thức \[A\] khi \[x = \frac{1}{9}.\]
c) Chứng minh rằng \[B = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\].
d) Đặt \[P = A.B.\] Tìm \[x \in \mathbb{N}\] để \[P\] có giá trị lớn nhất.
Cho biểu thức \[A = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\] và \[B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\].
a) Tìm điều kiện xác định của biểu thức \[A\] và \[B.\]
b) Tính giá trị của biểu thức \[A\] khi \[x = \frac{1}{9}.\]
c) Chứng minh rằng \[B = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\].
d) Đặt \[P = A.B.\] Tìm \[x \in \mathbb{N}\] để \[P\] có giá trị lớn nhất.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Với mọi \(x \ge 0,\) ta có:
⦁ \[\sqrt x - 3 \ne 0\] khi \(\sqrt x \ne 3\) hay \(x \ne 9.\)
⦁ \(x - 1 = \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\) và \(1 - \sqrt x = - \left( {\sqrt x - 1} \right)\)
Với mọi \(x \ge 0,\) ta có \(\sqrt x \ge 0\) nên \(\sqrt x + 1 \ge 1 > 0.\)
Do đó \(x - 1 \ne 0\) khi \(\sqrt x - 1 \ne 0,\) hay \(\sqrt x \ne 1,\) tức là \(x \ne 1.\)
Như vậy, điều kiện xác định của biểu thức \[A = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\] là \[x \ge 0,\,\,x \ne 9\] và điều kiện xác định của biểu thức \[B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\] là \[x \ge 0,\,\,x \ne 1.\]
b) Thay \[x = \frac{1}{9}\] (thỏa mãn điều kiện) vào biểu thức \[A\], ta được:
\[A = \frac{{\sqrt {\frac{1}{9}} - 1}}{{\sqrt {\frac{1}{9}} - 3}} = \frac{{\frac{1}{3} - 1}}{{\frac{1}{3} - 3}} = \frac{{ - \frac{2}{3}}}{{ - \frac{8}{3}}} = \frac{1}{4}.\]
Vậy \(A = \frac{1}{4}\) khi \(x = \frac{1}{9}.\)
c) Với \[x \ge 0;x \ne 1\], ta có:
\[B = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} - \frac{5}{{1 - \sqrt x }} + \frac{4}{{x - 1}}\]
\[ = \frac{{\sqrt x + 3}}{{\sqrt x + 1}} + \frac{5}{{\sqrt x - 1}} + \frac{4}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{5\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{4}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{x + 2\sqrt x - 3 + 5\sqrt x + 5 + 4}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{x + 7\sqrt x + 6}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]\[ = \frac{{x + \sqrt x + 6\sqrt x + 6}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\[ = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 6} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\].
Vậy với \[x \ge 0;x \ne 1\] thì \[B = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\].
d) Với \[x \ge 0,\,\,x \ne 1,x \ne 9,\] ta có:
\[P = A \cdot B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}} \cdot \frac{{\sqrt x + 6}}{{\sqrt x - 1}} = \frac{{\sqrt x + 6}}{{\sqrt x - 3}} = \frac{{\sqrt x - 3 + 9}}{{\sqrt x - 3}} = 1 + \frac{9}{{\sqrt x - 3}}.\]
⦁ Với \[0 \le x < 9,x \ne 1\] thì \[\sqrt x - 3 < 0\], suy ra \[1 + \frac{9}{{\sqrt x - 3}} < 1\] hay \[P < 1.\]
⦁ Với \[x > 9\] và \[x \in \mathbb{N}\] suy ra \[x \ge 10\]. Do đó, \[\sqrt x - 3 \ge \sqrt {10} - 3 > 0\].
Suy ra \[\frac{9}{{\sqrt x - 3}} \le \frac{9}{{\sqrt {10} - 3}}\] nên \[1 + \frac{9}{{\sqrt x - 3}} \le 1 + \frac{9}{{\sqrt {10} - 3}}\] hay \[P \le 1 + \frac{9}{{\sqrt {10} - 3}}\].
Dấu “=” xảy ra khi \[x = 10\].
Vậy với \[x = 10\] thì biểu thức \[P\] đạt giá trị lớn nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
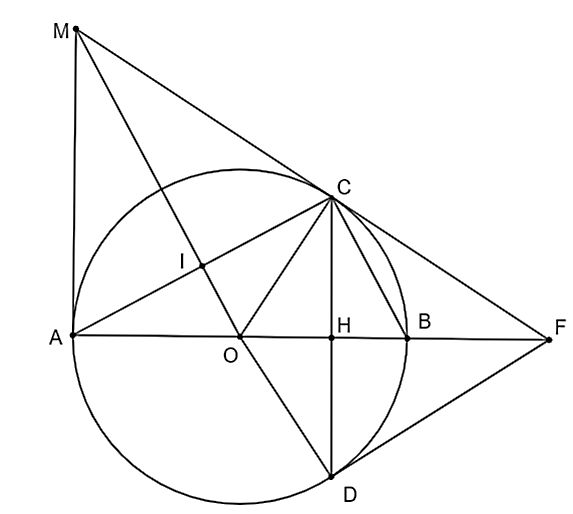
a) Xét \[\Delta OCD\] có: \[OC = OD = R\] nên \[\Delta OCD\] cân tại \[O.\]
Mà \[OH\] là đường cao của \[\Delta OCD\] nên \[OH\] cũng là đường phân giác của tam giác, nên \[\widehat {COF} = \widehat {DOF}.\]
Xét \[\Delta COF\] và \[\Delta DOF\] có:
\[OC = OD,\] \[\widehat {COF} = \widehat {DOF}\] và \[OF\] là cạnh chung.
Do đó, \[\Delta COF = \Delta DOF\] (c.g.c)
Suy ra \[\widehat {OCF} = \widehat {ODF}\] (hai góc tương ứng)
Mà \[\widehat {OCF} = 90^\circ \] (do \[OC \bot MF\]) nên \[\widehat {ODF} = 90^\circ \] hay \[FD \bot OD\] tại \[D\].
Xét đường tròn \[\left( {O;R} \right)\] có: \[FD \bot OD\] tại \[D\] và \[D \in \left( {O;R} \right)\]
Suy ra \[FD\] là tiếp tuyến của đường tròn \[\left( {O;R} \right)\] tại \[D\].
b) Xét đường tròn \[\left( {O;R} \right)\] có \[MA\] và \[MC\] là hai tiếp tuyến cắt nhau tại \[M\] nên \(MA = MC.\) Do đó \(M\) thuộc đường trung trực của \(AC.\)
Ta có: \[OA = OC = R\] nên \(O\) thuộc đường trung trực của \(AC.\)
Như vậy, \(OM\) là đường trung trực của \[AC\] nên \(OM \bot AC.\)
Xét \(\Delta ABC\) có \(CO\) là đường trung tuyến ứng với cạnh \(AB\) và \(CO = R = \frac{{AB}}{2}\) nên \(\Delta ABC\) vuông tại \(C\) hay \(BC \bot AC\).
Từ đó suy ra \(OI\,{\rm{//}}\,BC.\)
Xét \[\Delta ABC\] có \[O\] là trung điểm của \[AB\] và \(OI\,{\rm{//}}\,BC\) nên \[OI\] là đường trung bình của \[\Delta ABC\].
Suy ra \[OI = \frac{1}{2}BC\] (tính chất đường trung bình) hay \[BC = 2OI\].
c) ⦁ Xét tam giác \[MOC\] vuông tại \[C\], có: \[\cos \widehat {MOC} = \frac{{OC}}{{MO}} = \frac{R}{{2R}} = \frac{1}{2},\] suy ra \[\widehat {MOC} = 60^\circ \].
Do \(MA,\,\,MC\) là hai tiếp tuyến cắt nhau tại \(M\) của đường tròn \(\left( {O;R} \right)\) nên \(OM\) là tia phân giác của \[\widehat {AOC}\]. Suy ra \[\widehat {AOC} = 2\widehat {MOC} = 2 \cdot 60^\circ = 120^\circ \].
Do đó \[\widehat {COB} = 180^\circ - \widehat {AOC} = 180^\circ - 120^\circ = 60^\circ \].
⦁ Ta có \[F\] là giao điểm của hai tiếp tuyến tại \[C\] và \[D\] nên \[OF\] là tia phân giác của \[\widehat {DOC}\].
Suy ra \[\widehat {DOC} = 2\widehat {COB} = 2 \cdot 60^\circ = 120^\circ .\]
Diện tích hình quạt giới hạn bởi bán kính \[OC,OD\] và cung nhỏ \[CD\] là
\[{S_1} = \frac{{120 \cdot \pi \cdot {R^2}}}{{360}} = \frac{{\pi {R^2}}}{3}\] (đơn vị diện tích).
⦁ Xét \(\Delta OCH\) vuông tại \(H\) ta có: \(CH = OC \cdot \sin \widehat {COB} = R \cdot \sin 60^\circ = \frac{{R\sqrt 3 }}{2};\)
\(OH = OC \cdot \cos \widehat {COB} = R \cdot \cos 60^\circ = \frac{R}{2}.\)
Xét \(\Delta OCD\) cân tại \(O\) (do \(OC = OD)\) nên đường phân giác \(OH\) cũng đồng thời là đường trung tuyến, nên \(H\) là trung điểm của \(CD,\) suy ra \(CD = 2CH = 2 \cdot \frac{{R\sqrt 3 }}{2} = R\sqrt 3 .\)
Diện tích tam giác \(OCD\) là: \({S_2} = \frac{1}{2}OH \cdot CD = \frac{1}{2} \cdot \frac{R}{2} \cdot R\sqrt 3 = \frac{{{R^2}\sqrt 3 }}{4}\) (đơn vị diện tích).
Diện tích hình được giới hạn bởi dây \(CD\) và cung nhỏ \[CD\] là:
\(S = {S_1} - {S_2} = \frac{{\pi {R^2}}}{3} - \frac{{{R^2}\sqrt 3 }}{4} = \frac{{{R^2}\left( {4\pi - 3\sqrt 3 } \right)}}{{12}}\) (đơn vị diện tích).
Vậy diện tích hình được giới hạn bởi dây \(CD\) và cung nhỏ \[CD\] là\(\frac{{{R^2}\left( {4\pi - 3\sqrt 3 } \right)}}{{12}}\) (đvdt).
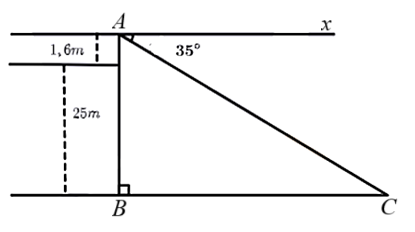
Lời giải
⦁ Gọi x (m) và y (m) các kích thước hình chữ nhật mà tể tướng sẽ căng \[\left( {0 < x < 150;\,\,0 < y < 150} \right).\]
Khi đó, ta có chu vi của mảnh đất hình chữ nhật đó là 300 mét, suy ra ![]()
Diện tích của mảnh đất là ![]() .
.
⦁ Chứng minh bổ đề: 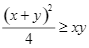 với mọi x > 0, y > 0
với mọi x > 0, y > 0
Thật vậy, với mọi ta có:
![]()
![]()
![]()
![]()
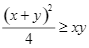 .
.
Đẳng thức xảy ra khi ![]()
⦁ Áp dụng bất đẳng thức trên, ta có:
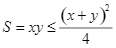
Suy ra ![]() .
.
Dấu bằng xảy ra khi ![]() (thỏa mãn).
(thỏa mãn).
Khi đó, diện tích lớn nhất S = 5 625 m2 khi x = y = 75 m
Vậy tể tướng đó cần căng sợi dây bao quanh mảnh đất hình hình vuông có cạnh 75 m để mảnh đất nhận được có diện tích lớn nhất.
Câu 3
Giải bài toán sau bằng cách lập hệ phương trình:
Giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu tổng cộng là 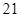 triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi
triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi 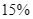 và nồi chiên không dầu giảm giá
và nồi chiên không dầu giảm giá 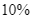 so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết
so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết 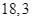 triệu. Tính giá niêm yết của mỗi sản phẩm.
triệu. Tính giá niêm yết của mỗi sản phẩm.
Giải bài toán sau bằng cách lập hệ phương trình:
Giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu tổng cộng là ![]() triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi
triệu đồng. Nhân dịp khuyến mãi cuối năm, cửa hàng giảm giá bếp từ đôi ![]() và nồi chiên không dầu giảm giá
và nồi chiên không dầu giảm giá ![]() so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết
so với giá niêm yết nên bác Lan đi mua hai sản phẩm này chỉ hết ![]() triệu. Tính giá niêm yết của mỗi sản phẩm.
triệu. Tính giá niêm yết của mỗi sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.