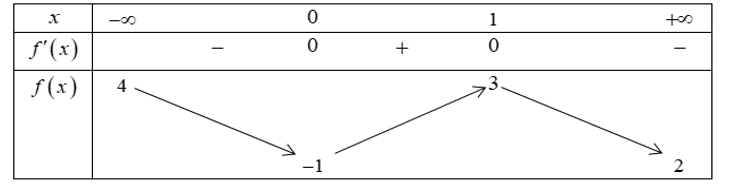
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau
Biết đồ thị hàm số \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x} - x} \right)\) có hai đường tiệm cận ngang là \(y = a\) và \(y = b\), trong đó \(a < b\). Tính \(S = a - 100b\).
Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên như sau

Biết đồ thị hàm số \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x} - x} \right)\) có hai đường tiệm cận ngang là \(y = a\) và \(y = b\), trong đó \(a < b\). Tính \(S = a - 100b\).
Quảng cáo
Trả lời:
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + 2x} - x} \right) = 1\) và \(f\left( 1 \right) = 3\), suy ra \(\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } f\left( {\sqrt {{x^2} + 2x} - x} \right) = 3\).
\(\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 2x} - x} \right) = + \infty \) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\), suy ra \(\mathop {\lim }\limits_{x \to - \infty } g\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } f\left( {\sqrt {{x^2} + 2x} - x} \right) = 2\).
Vậy đồ thị hàm số \(g\left( x \right)\) có \(2\) đường tiệm cận ngang \(y = 2\) và \(y = 3\). Suy ra \(a = 2,\,b = 3\).
Suy ra \(S = a - 100b = - 298\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vị trí của máy bay sau 5 phút tiếp theo là \(C(x;y;z)\).
Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng.
Do vận tốc của máy bay không đổi và thời gian bay từ \(A\) đến \(B\) gấp đôi thời gian bay từ \(B\) đến \(C\) nên \(AB = 2BC\).
Do đó \(\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AB} = \left( {\frac{{940 - 800}}{2};\frac{{550 - 500}}{2};\frac{{9 - 7}}{2}} \right) = \left( {70;25;1} \right)\).
Mặt khác, \(\overrightarrow {BC} = (x - 940;y - 550;z - 9)\) nên \(\left\{ {\begin{array}{*{20}{l}}{x - 940 = 70}\\{y - 550 = 25}\\{z - 9 = 1}\end{array}} \right.\)
Từ đó \(\left\{ {\begin{array}{*{20}{l}}{x = 1010}\\{y = 575}\\{z = 10}\end{array}} \right. \Rightarrow x + y + z = 1595\).
Lời giải
a) S, b) S, c) Đ, d) S
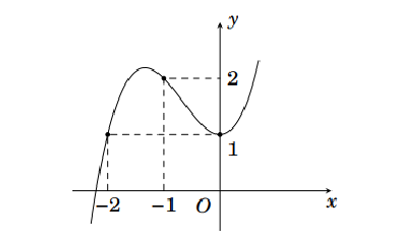
a) Dựa vào đồ thị ta thấy hàm số đồng biến trên khoảng \(\left( { - \infty ;{x_0}} \right)\) với \( - 2 < {x_0} < - 1\).
b) Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} = 1\).
c) Đồ thị hàm số cắt trục Oy tại điểm có tọa độ \(\left( {0;1} \right)\).
d) Đồ thị đi qua ba điểm \(\left( { - 2;1} \right),\left( { - 1;2} \right),\left( {0;1} \right)\) và đạt cực trị tại \(x = 1\) nên ta có hệ:
\(\left\{ \begin{array}{l} - 8a + 4b - 2c + d = 1\\ - a + b - c + d = 2\\d = 1\\c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 0\\d = 1\end{array} \right. \Rightarrow 2a + 3b + c = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
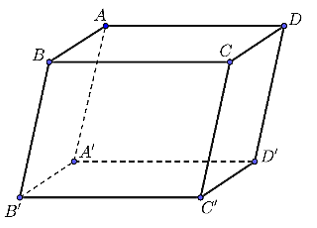
A. \(2\overrightarrow {AA'} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.